Question

Two ships are sailing in the sea on either side of a light-house. The angle of depression of the two ships is \[{{45}^{\circ }}\] each. If the height of the light house is 300 m, then the distance between ships is:
A. 600 m
B. \[600\sqrt{3}m\]
C. \[300\sqrt{3}m\]
D. 300 m

Answer 1

Hint:
Draw the figure as per mentioned in the question. Given are angles of depression from top of lighthouse to both ships. Consider the two triangles formed and use the trigonometric ratios for the calculation of the distance between both ships.

Complete step-by-step answer:

We have been given two ships that are sailing in the sea on either side of a lighthouse.

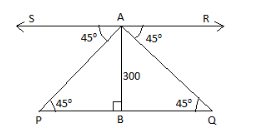
Let AB be the light house. We have been given the height of the lighthouse as 300 m.
\[\therefore \]Height of light house = AB = 300 m
Let P and Q be the two ships on either side of the lighthouse AB.
From the figure we can say that PQ is parallel to RS, i.e. \[PQ||RS\].
We have been given the angle of depression of 2 ships to be \[{{45}^{\circ }}\] each.
\[\therefore \angle SAP={{45}^{\circ }}\] and \[\angle RAQ={{45}^{\circ }}\].
As \[PQ||RS\], we can say that \[\angle SAP=\angle APB={{45}^{\circ }}\] and \[\angle RAQ=\angle AQB={{45}^{\circ }}\], i.e. \[\angle SAP=\angle APB\] are alternate angles. Similarly, \[\angle RAQ=\angle AQB\] are alternate angles.
Now let us first consider \[\Delta PAB\].
\[\tan {{45}^{\circ }}=\dfrac{perpendicular}{base}=\dfrac{300}{PB}\]
We know that tan45 = 1, from the trigonometric table.
\[\therefore 1=\dfrac{300}{PB}\Rightarrow PB=300m.\]
Now let us consider \[\Delta QAB\].
\[\tan {{45}^{\circ }}=\dfrac{perpendicular}{base}=\dfrac{300}{BQ}\]
\[1=\dfrac{300}{BQ}\] \[\because \tan {{45}^{\circ }}=1\]
\[\therefore BQ=300m.\]
We need to find the distance between the ships, i.e. we need to find the length of PQ. From the figure, we can say that,
PQ = PB + BQ
We found that PB = 300 m, BQ = 300m.
\[\therefore \]PQ = PB + BQ = 300 + 300 = 600 m.
Thus we got the distance between two ships as 600 m.
Option A is the correct answer.

Note: The angles given are the angle of depression. Take sea level parallel to the height of the light house, so we can convert the angle of depression to angle to angle of elevation, thus making calculations easier. They become alternate angles as it is parallel.