Question

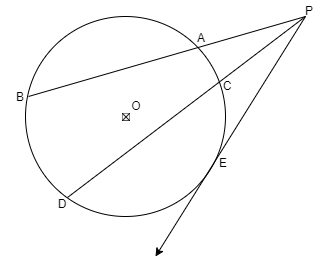
Two secant segments,\[\overline {PAB} \] and\[\overline {PCD} \], and a tangent segment,$\overline {PE} $ are drawn to a circle from an external point P. If PB = 9cm, PD = 12cm, and the external segment of \[\overline {PAB} \] is 1 centimeter longer than the external segment of\[\overline {PCD} \], find PE.

Answer 1

Hint: Remember to use the equation $PA(PB) = {(PE)^2}$ and \[PC(PD) = {(PE)^2}\] also use the given statement i.e. external segment of \[\overline {PAB} \] is 1 centimeter longer than the external segment of\[\overline {PCD} \] to form an equation and to find the value of PE.

Complete step by step solution:
Given in the question
PB = 9cm, PD = 12cm
PA (external segment of\[\overline {PAB} \]) = 1cm + PC (external segment of\[\overline {PCD} \]) --- (equation 1)
Now we know that
$PA(PB) = {(PE)^2}$ --- (Equation 2)
Similarly
\[PC(PD) = {(PE)^2}\] ---- (Equation 3)
From equation 2 and 3
$PA(PB) = PC(PD)$
$ \Rightarrow $$PA(9) = PC(12)$
From equation 1
(1 + PC) 9 = PC (12)
9 + 9PC = 12PC
9 = 3PC
PC = 3
Now,
\[PA\left( 9 \right){\text{ }} = {\text{ }}12 \times PC\]
\[PA{\text{ }} = {\text{ }}\dfrac{{12 \times 3}}{9}\]
PA = 4
${\left( {PE} \right)^2} = \left( {PA} \right)\left( {PB} \right)$
${\left( {PE} \right)^2} = \left( 4 \right)\left( 9 \right)$
PE = 6
Hence the value of PE = 6cm
Note: In these types of questions use the given information to make the equation i.e. (PA (external segment of\[\overline {PAB} \]) = 1cm + PC (external segment of\[\overline {PCD} \])) then since we know that $PA(PB) = {(PE)^2}$similarly \[PC(PD) = {(PE)^2}\]using these equations find the value of PC and using the value of PC find the value of PA and PE.