Question

Two poles of equal height are standing opposite to each other on either side of a road which is 100m wide. From a point between them on the road, angles of elevation of their tops are \[{{30}^{\circ }}\] and \[{{60}^{\circ }}\]. The height of each pole in meter is: -
(a) \[25\sqrt{3}\]
(b) \[20\sqrt{3}\]
(c) \[28\sqrt{3}\]
(d) \[30\sqrt{3}\]

Answer 1

Hint: Draw a diagram of the given situation. Assume the height of each pillar as ‘h’. Assume a point in between the two pillars whose distance from pillar 1 and pillar 2 are \[{{x}_{1}}\] and \[{{x}_{2}}\] respectively. Form two right angle triangles and use, \[\tan \theta \] = (perpendicular / base), where \[\theta \] is the angle of elevation, to form expressions in terms of \[{{x}_{1}}\] and \[{{x}_{2}}\] and equate their with 100 to determine the value of h.

Complete step by step answer:
Let us draw a diagram of the given situation.

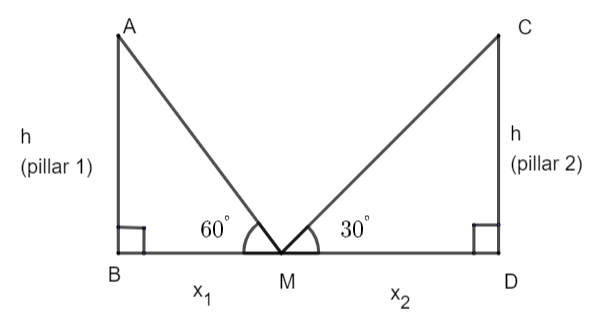
In the above figure, we have assumed AB and CD as pillar 1 and pillar 2 respectively. We have assumed their height as ‘h’. The angle of elevation of pillar 1 and pillar 2 are \[{{60}^{\circ }}\] and \[{{30}^{\circ }}\] respectively. We have assumed a point M whose distance from foot of pillar 1 and pillar 2 are \[{{x}_{1}}\] and \[{{x}_{2}}\] respectively. Here, we have to determine the value of h.
Now, in right angle triangle CDM, we have,
CD = h
DM = \[{{x}_{2}}\]
\[\angle CMD={{30}^{\circ }}\]
Using, \[\tan \theta \] = (perpendicular / base), where \[\theta \] is the angle of elevation, we get,
\[\begin{align}
  & \Rightarrow \tan {{30}^{\circ }}=\dfrac{CD}{DM} \\
 & \Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{{{x}_{2}}} \\
\end{align}\]
\[\Rightarrow {{x}_{2}}=\dfrac{h}{\tan {{30}^{\circ }}}\] - (1)
Now, in right angle triangle ABM, we have,
AB = h
BM = \[{{x}_{1}}\]
\[\angle AMB={{60}^{\circ }}\]
Using, \[\tan \theta \] = (perpendicular / base), we get,
\[\begin{align}
  & \Rightarrow \tan {{60}^{\circ }}=\dfrac{AB}{BM} \\
 & \Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{{{x}_{1}}} \\
\end{align}\]
\[\Rightarrow {{x}_{1}}=\dfrac{h}{\tan {{60}^{\circ }}}\] - (2)
Here, in the above question we have been given that the distance between the two pillars is 100m.
\[\Rightarrow \] BD = 100
\[\begin{align}
  & \Rightarrow BM+DM=100 \\
 & \Rightarrow {{x}_{1}}+{{x}_{2}}=100 \\
\end{align}\]
Substituting the values of \[{{x}_{1}}\] and \[{{x}_{2}}\] from equations (1) and (2), we get,
\[\begin{align}
  & \Rightarrow \dfrac{h}{\tan {{30}^{\circ }}}+\dfrac{h}{\tan {{60}^{\circ }}}=100 \\
 & \Rightarrow h\left[ \dfrac{1}{\tan {{30}^{\circ }}}+\dfrac{1}{\tan {{60}^{\circ }}} \right]=100 \\
\end{align}\]
Substituting, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\] and \[\tan {{60}^{\circ }}=\sqrt{3}\], we get,
\[\begin{align}
  & \Rightarrow h\left[ \dfrac{1}{\dfrac{1}{\sqrt{3}}}+\dfrac{1}{\sqrt{3}} \right]=100 \\
 & \Rightarrow h\left[ \sqrt{3}+\dfrac{1}{\sqrt{3}} \right]=100 \\
\end{align}\]
\[\begin{align}
  & \Rightarrow h\times \left( \dfrac{4}{\sqrt{3}} \right)=100 \\
 & \Rightarrow h=\dfrac{100\times \sqrt{3}}{4} \\
 & \Rightarrow h=25\sqrt{3}m \\
\end{align}\]

So, the correct answer is “Option a”.

Note: One may note that we must draw the diagram so that we can visualize and understand the situation more clearly and easily. As you can see that we have used the trigonometric function \[\tan \theta \] and not \[\sin \theta \] or \[\cos \theta \] in the two right angle triangles. This is because we have been provided with the information regarding base and perpendicular but not the hypotenuse of the triangle.