Question

Two poles, 18m and 13m high, stand upright in a playground. If their feet are $12$ m apart find the distance between their tops.

Answer 1

Hint: First we will convert the given data into a pictorial format and note down all the given values. After dividing the obtained diagram into two identical shapes we will get the way to find the required value. By using the Pythagoras theorem and the given data in the question, we will find the required value.

Complete step by step solution:
Given that, two poles of height $18$ m and $13$ m are standing in an upright position in a playground. Let $AB$ is the first pole of height $18$ m and $DC$ be the second pole of height $13$ m. Now the diagrammatically we can visualize them as given below.

Again, we have given that the distance between the two poles at the bottom is $12$ m i.e. in the above diagram we have the value of $AC$ as $12$ m, now the diagram will change as

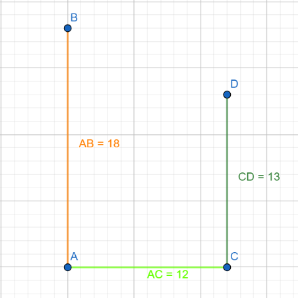
Now we have to calculate the distance between the top of two poles i.e. from the diagram we need to calculate the value of $BD$ which is inclined with some angle. For this, we are going to construct a perpendicular line from point $D$ to the line $AB$ which is parallel and equal to the line $AC$ as shown in the below figure.

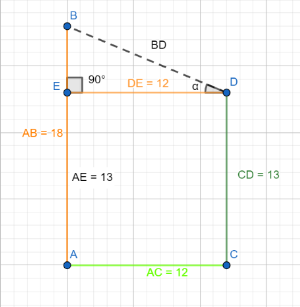
So here we can divide the above diagram into two identical shapes: they are $ACDE$ rectangle and $EDB$ right angle triangle. In the diagram we have the values
$AB=18$m
$CD=AE=13$m
$AC=DE=12$m
$\begin{align}
  & BE=AB-AE \\
 & \Rightarrow BE=18-13 \\
 & \Rightarrow BE=5\text{ m} \\
\end{align}$
Let the value of $BD=x$ m which is the distance between the tops of the poles.
In the diagram we have a right angle triangle $EDB$ and the sides of the right angle triangle are $BE=5\text{ m}$, $DE=12\text{ m}$ now from the Pythagoras theorem we can write
$\text{Hypotenuse}{{\text{e}}^{2}}=\text{sid}{{\text{e}}^{2}}+\text{sid}{{\text{e}}^{2}}$
In the right angle triangle $EDB$the hypotenuse is $BD$ which is equal to $x$ m.
$\begin{align}
  & \therefore B{{D}^{2}}=E{{D}^{2}}+B{{E}^{2}} \\
 & \Rightarrow {{x}^{2}}={{12}^{2}}+{{5}^{2}} \\
 & \Rightarrow {{x}^{2}}=144+25 \\
 & \Rightarrow {{x}^{2}}=169 \\
 & \Rightarrow x=\sqrt{169} \\
 & \therefore x=13\text{ m} \\
\end{align}$
$\therefore $ The distance between the top of the two poles is $13$ m.

Note: In the problem they have mentioned to calculate the distance between the two poles, so we have calculated the inclined distance between the tops of poles. If they have asked to calculate the perpendicular distance between them then we had to write the value of $DE=12$m as the required value.