Question

Two pillars of equal height stand on either side of a road-way which is 60 m wide. At a point in the road-way between the pillars, the elevation of the top of the pillars is $ {{60}^{\circ }} $ and $ {{30}^{\circ }} $ . The height of the pillar is
A. $ 15\sqrt{3}\text{ }m $
B. $ \dfrac{15}{\sqrt{3}}\text{ }m $
C. $ 15\text{ }m $
D. $ 20\text{ }m $

Answer 1

Hint: We first assume the height of the pillars. We then use trigonometric ratios for the given angles to find the relation between the base and the height of the pillars. We then form the equation and solve that to find the height of the pillars.

Complete step-by-step answer:
We first try to draw the scenario for the pillars.

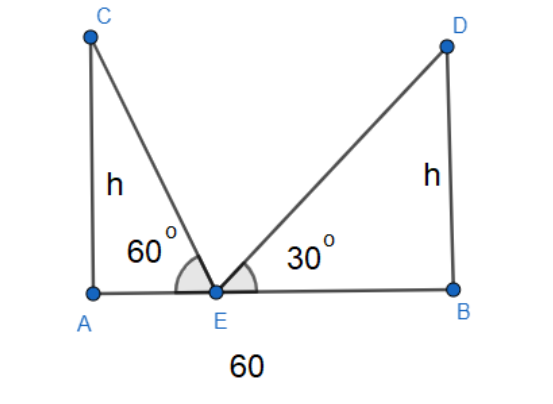
The pillars are AC and BD. We assume the length of both of the pillars to be $ h $ .
The distance between the points A and B is 60 m. So, $ AB=60 $ .
At a point E in the road-way between the pillars, the elevation of the top of the pillars is $ {{60}^{\circ }} $ and $ {{30}^{\circ }} $ to the points C and D respectively. So, $ \angle CEA={{60}^{\circ }},\angle DEB={{30}^{\circ }} $ .
Now with respect to the angles $ \angle CEA={{60}^{\circ }},\angle DEB={{30}^{\circ }} $ and the equal sides of AC and BD, we find the length of the segments AE and BE.
We have
 $ \begin{align}
  & \dfrac{AE}{AC}=\cot \left( \angle CEA \right)=\cot {{60}^{\circ }} \\
 & \dfrac{BE}{BD}=\cot \left( \angle DEB \right)=\cot {{30}^{\circ }} \\
\end{align} $
We place the values to get
 $ \begin{align}
  & \dfrac{AE}{h}=\cot {{60}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
 & \dfrac{BE}{h}=\cot {{30}^{\circ }}=\sqrt{3} \\
\end{align} $
On simplification we get $ AE=\dfrac{h}{\sqrt{3}},BE=h\sqrt{3} $ .
We know $ AE+BE=AB=60 $ . Putting the values, we get
 $ \begin{align}
  & \dfrac{h}{\sqrt{3}}+h\sqrt{3}=60 \\
 & \Rightarrow \dfrac{4h}{\sqrt{3}}=60 \\
 & \Rightarrow h=\dfrac{60\times \sqrt{3}}{4}=15\sqrt{3} \\
\end{align} $
The length of the pillars is $ 15\sqrt{3} $ . The correct option is A.
So, the correct answer is “Option A”.

Note: In the relation we will take that particular trigonometric ratio which gives the unknowns as the numerator form. That particular ratio gives a direct answer for the unknown. Also, we could use the ratios as the triangles were right angle triangles.