Question

Two people standing on the same side of a tower in straight line with it, measures the angles of elevation of the height of tower as \[{{25}^{\circ }}\] and \[{{50}^{\circ }}\] respectively. If the height of the tower is 70m, find the distance between the two people.

Answer 1

Hint: Draw a diagram of the given conditions and assume the height of the tower as ‘h’. Assume \[{{x}_{1}}\] and \[{{x}_{2}}\] as the distance of person 1 and person 2 respectively from the foot of the tower. Form two right-angle triangles and use \[\tan \theta \] = (perpendicular / base) to form expressions in terms of \[{{x}_{1}}\] and \[{{x}_{2}}\], where ‘\[\theta \]’ is the angle of elevation. Take the difference of \[{{x}_{1}}\] and \[{{x}_{2}}\] and substitute the given values of \[\theta \] and ‘h’ to get the answer.

Complete step by step answer:
Let us draw a rough diagram of the given situation: -

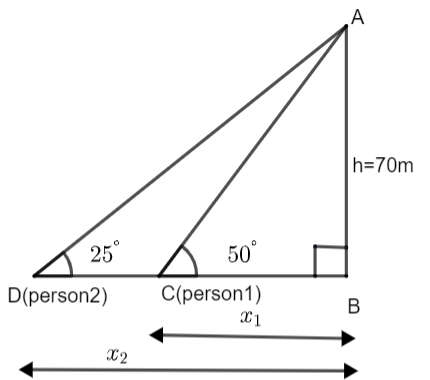
In the above figure, we have assumed that AB is the tower of height ‘h’. A is the top of the tower and B is its foot. Here, person 1 is assumed to be standing at point C at a distance of \[{{x}_{1}}\] from point B. Person 2 is assumed to be at point D at a distance of \[{{x}_{2}}\] from point B. The angle of elevation of the top of the tower for person 1 and person 2 are \[{{50}^{\circ }}\] and \[{{25}^{\circ }}\] respectively.
Now, in the right angle triangle ABC, we have,
AB = h
BC = \[{{x}_{1}}\]
\[\angle ACB={{50}^{\circ }}\]
Using, \[\tan \theta \] = (perpendicular / base), where \[\theta \] is the angle of elevation, we get,
\[\begin{align}
  & \Rightarrow \tan {{50}^{\circ }}=\dfrac{AB}{BC} \\
 & \Rightarrow \tan {{50}^{\circ }}=\dfrac{h}{{{x}_{1}}} \\
\end{align}\]
\[\Rightarrow {{x}_{1}}=\dfrac{h}{\tan {{50}^{\circ }}}\] - (1)
Now, in right angle triangle ABD, we have,
AB = h
BD = \[{{x}_{2}}\]
\[\angle ADB={{25}^{\circ }}\]
Using, \[\tan \theta \] = (perpendicular / base), we get,
\[\Rightarrow \tan {{25}^{\circ }}=\dfrac{h}{{{x}_{2}}}=\dfrac{AB}{BD}\]
\[\Rightarrow {{x}_{2}}=\dfrac{h}{\tan {{25}^{\circ }}}\] - (2)
Now, we can clearly see that the total distance between the two people is \[CD=BD-BC={{x}_{2}}-{{x}_{1}}\]. So, subtracting equations (2) and (1), we get,

\[\begin{align}
  & \Rightarrow {{x}_{2}}-{{x}_{1}}=\dfrac{h}{\tan {{25}^{\circ }}}-\dfrac{h}{\tan {{50}^{\circ }}} \\
 & \Rightarrow {{x}_{2}}-{{x}_{1}}=h\left[ \dfrac{1}{\tan {{25}^{\circ }}}-\dfrac{1}{\tan {{50}^{\circ }}} \right] \\
\end{align}\]
Using the conversion, \[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\], we get,
\[\Rightarrow {{x}_{2}}-{{x}_{1}}=h\left[ \dfrac{\cos {{25}^{\circ }}}{\sin {{25}^{\circ }}}-\dfrac{\cos {{50}^{\circ }}}{\sin {{50}^{\circ }}} \right]\]
Substituting h = 70, we get,
\[\Rightarrow {{x}_{2}}-{{x}_{1}}=70\times \left[ \dfrac{\sin {{25}^{\circ }}\cos {{25}^{\circ }}-\cos {{50}^{\circ }}\sin {{50}^{\circ }}}{\sin {{25}^{\circ }}\sin {{50}^{\circ }}} \right]\]
Using the identity, \[\sin A\cos B-\cos A\sin B=\sin \left( A-B \right)\], we get,
\[\begin{align}
  & \Rightarrow {{x}_{2}}-{{x}_{2}}=70\times \left[ \dfrac{\sin \left( {{50}^{\circ }}-{{25}^{\circ }} \right)}{\sin {{25}^{\circ }}\sin {{50}^{\circ }}} \right] \\
 & \Rightarrow {{x}_{2}}-{{x}_{2}}=70\times \dfrac{\sin {{25}^{\circ }}}{\sin {{25}^{\circ }}\sin {{50}^{\circ }}} \\
\end{align}\]
Cancelling the common factor, we get,
\[\Rightarrow {{x}_{2}}-{{x}_{2}}=\dfrac{70}{\sin {{50}^{\circ }}}\]
Hence, the distance between two people is \[\dfrac{70}{\sin {{50}^{\circ }}}\].

Note:
 One may note that we have obtained the answer in terms of the sine of the angle \[{{50}^{\circ }}\]. This is because we cannot substitute the value of \[\sin {{50}^{\circ }}\] in the expression without using a sine table. So, the expression cannot be simplified any further. You must draw a diagram according to the given question so that all the conditions can be easily visualized. Also, note that we have used \[\tan \theta \] and not \[\sin \theta \] or \[\cos \theta \] while solving the question because we have been provided information regarding base and perpendicular but not the hypotenuse.