Question

Two particles P and Q are moving on a circle. At a certain instant of time both the particles are diametrically opposite and P has tangential acceleration $8m/{s^2}$ and centripetal acceleration $5m/{s^2}$ whereas Q has only centripetal acceleration of $1m/{s^2}$. At that instant acceleration $(in{\text{ }}m/{s^2})$ of P with respect to Q is:
$
  (a){\text{ 14}} \\
  (b){\text{ }}\sqrt {80} \\
  (c){\text{ 10}} \\
  (d){\text{ 12}} \\
 $

Answer 1

Hint: In this question draw a free body diagram for the particle P and particle Q. Then write the vector equation representing the acceleration for both the particles P and Q. Then use the concept that the relative acceleration of P with respect to Q will be will the difference of accelerations of P and Q. Find the magnitude of this relative acceleration vector to get the right answer.

Complete Step-by-Step solution:

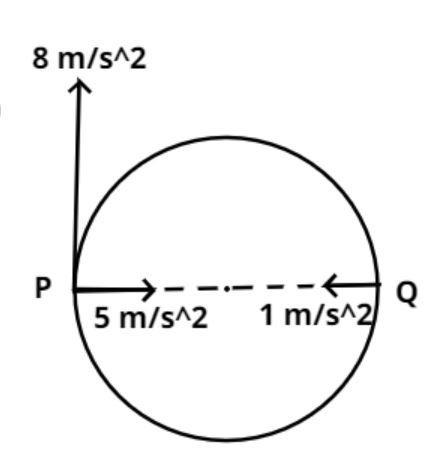
The particles P and Q diametrically opposite are shown in the above diagram.
Let the direction of acceleration in positive direction of x axis is ($\hat i$) and in negative direction of x axis is ($ - \hat i$), similarly let the direction of acceleration in positive direction of y axis is ($\hat j$) and in negative direction of y axis is ($ - \hat j$).
Now it is given P has tangential acceleration = $8m/{s^2}$ and centripetal acceleration = $5m/{s^2}$
Let P is on the left side of the Q as shown in figure and its tangential acceleration is in the positive direction of y-axis and we all know that the centripetal acceleration is always towards the center so the direction of centripetal acceleration is positive direction of x-axis.
So the acceleration of p is
${a_p} = 5\hat i + 8\hat j$ $m/{s^2}$
Now it is also given that Q has only centripetal acceleration = $1m/{s^2}$, and we all know that it is always towards the center so the direction of Q centripetal acceleration is negative towards the x-axis as shown in the figure.
So the acceleration of Q is
${a_Q} = - \hat i$ $m/{s^2}$
Now the relative acceleration is the difference of P and Q acceleration.
${a_{rel}} = {a_P} - {a_Q}$
$ \Rightarrow {a_{rel}} = 5\hat i + 8\hat j - \left( { - \hat i} \right) = 6\hat i + 8\hat j$ $m/{s^2}$
Now take the modulus of above equation we have,
$ \Rightarrow \left| {{a_{rel}}} \right| = \left| {6\hat i + 8\hat j} \right|$
$ \Rightarrow \left| {{a_{rel}}} \right| = \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10$ $m/{s^2}$
So this is the required relative velocity of particle P and Q respectively.
Hence option (C) is the correct answer.

Note – Trick point here is that when a body revolves around a circle then it undergoes influence of two different accelerations. The first one is tangential acceleration, it always acts tangentially and it’s direction is the same as the unique tangent possible at that point and the second acceleration is centripetal acceleration, this acceleration is always directed towards the center of the circle around which the particles are revolving.