Question

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both the particles are the same and equal to A and T, respectively. At time t=0, one particle is at displacement A while the other one has displacement \[\dfrac{-A}{2}\] and they are moving towards each other. If they cross each other at time t, then t is:
A. $\dfrac{5T}{6}$
B. $\dfrac{T}{4}$
C. $\dfrac{T}{3}$
D. $\dfrac{T}{6}$

Answer 1

Hint: We are given two particles performing SHM in a straight line about the same equilibrium point. It is said that their amplitude and time period are the same and we are given the position of the two particles at t = 0. We can find the initial phase difference between the particles and calculate the phase difference when they cross each other. Thus we can find the solution.

Complete step by step answer:
In the question it is said that there are two particles, which perform simple harmonic motion in a straight line about the same equilibrium point.
It is said that initially one particle is at a displacement A and the other is at displacement $-\dfrac{A}{2}$, where A is the amplitude. It is also said that these particles are moving towards each other.
Let us find the initial phase between the two particles. For that consider the figure given below which shows the initial situation.

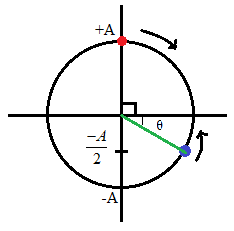
From the figure we can see that ‘$\theta +90{}^\circ $’ is the phase angle here.
From the figure we can calculate ‘$\theta $’ as,
$\sin \theta =\dfrac{\left( \dfrac{A}{2} \right)}{A}$
$\Rightarrow \sin \theta =\dfrac{1}{2}$
$\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{1}{2} \right)$
$\Rightarrow \theta =30{}^\circ $
Therefore we have the initial phase as $30{}^\circ +90{}^\circ =120{}^\circ $
In the question it is said that the time period of the two particles are the same.
We know that if the time period is the same, then the angular velocity will also be the same.
When they have the same angular velocity, we can say that both the particles will travel the same distance at the same time.
Since the total initial phase angle between the particles is $120{}^\circ $, we can say that the phase angle covered by each particle will be half of the total initial phase, i.e. $60{}^\circ $.
We are given the total time period of the two particles at ‘T’. we know that time period is the time taken for one complete rotation, i.e. $360{}^\circ $.
Therefore the time taken to complete $360{}^\circ $ is T, then the time taken to travel $60{}^\circ $ will be,
$\Rightarrow \dfrac{T}{360}\times 60$
$\Rightarrow \dfrac{T}{36}\times 6$
$\Rightarrow \dfrac{T}{6}$
Therefore the time at which both the particles will cross each other is $\dfrac{T}{6}$.

So, the correct answer is “Option D”.

Note: In this question we say that when the time periods of the two particles in simple harmonic motion are the same, then their angular velocities will also be the same.
We know that the relation between time period and angular velocity is given as,
$T=\dfrac{2\pi }{\omega }$, where ‘T’ is the time period and ‘$\omega $’ is the angular velocity.
From this we can see that time period only depends upon angular velocity.
So when two particles have the same time period, then they will have the same angular velocity.