Question

Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is:

$\begin{align}
  & \text{A}\text{. 0} \\
 & \text{B}\text{. 2}\pi \text{/3} \\
 & \text{C}\text{. }\pi \\
 & \text{D}\text{. }\pi /6 \\
\end{align}$

Answer 1

Hint: First find the equation for amplitude for the two particles following simple harmonic motion, then find out the values which are the same in both the equation. Find the total phase difference between the two-particles. Then place the value of amplitude given in the question. And find the value of the particles in the first phase and then calculate the value of the phase of the particles in the second phase. Differentiate the two values to find the correct answer.

Complete answer:

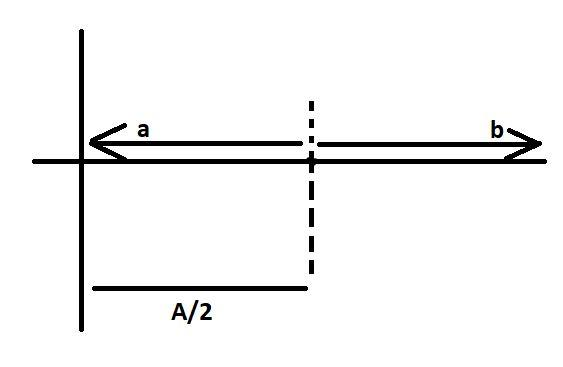
Here in the above diagram, we see two particles ‘a’ and ‘b’ are traveling in the opposite direction when both the body reaches a position that is half the amplitude (A/2). We are considering the position from where both the particles started traveling in the opposite direction as the mean position.

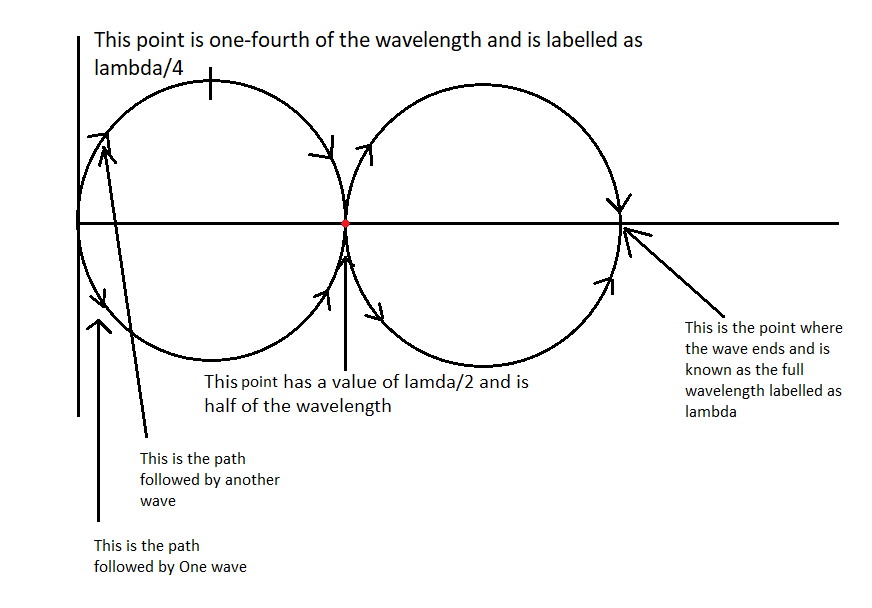
We see that there are two waves and one of the waves is traveling in a positive direction and another one in the negative direction. Both the waves are meeting at a point that is marked in the red.
So we can say according to SHM,
$a=A\sin \left( \omega t+{{\phi }_{1}} \right)$ ….. eq.1
$b=A\sin \left( \omega t+{{\phi }_{2}} \right)$
We know that the value of omega is the same for both the particle though particle ‘a’ is positive and particle ‘b’ is negatively propagating.
So we can say that the phase difference between the two particles must be,
$\left( \omega t+{{\phi }_{1}} \right)-\left( \omega t+{{\phi }_{2}} \right)=\pi $,

As it is dependent on the sin curve, so before the curve reaches $\pi $ angle the curve will be positive and after that it will be negative so the phase difference is $\pi $.

Now we know that,
$a=\dfrac{A}{2}$,
Now, taking eq.1
$a=A\sin \left( \omega t+{{\phi }_{1}} \right)$,
$\dfrac{A}{2}=A\sin \left( \omega t+{{\phi }_{1}} \right)$.,
So,$\sin \dfrac{\pi }{6}=\dfrac{1}{2}$ , so the angle must be 1/2.
$\left( \omega t+{{\phi }_{1}} \right)=\dfrac{\pi }{6}$…. In phase 1.
In phase 2,
$\pi -\dfrac{\pi }{6}=\dfrac{5\pi }{6}$…. In phase 2.
So the phase difference must be,
$\dfrac{5\pi }{6}-\dfrac{\pi }{6}=\dfrac{4\pi }{6}=\dfrac{2\pi }{3}$ .

So, the correct answer is “Option B”.

Note:
In the question it is said that the frequency for both the particles is the same, if the frequency is the same then the time period must be the same, if a time period is the same then omega and amplitude must also be the same.