
Two particles A and B, each of mass m are kept stationary by applying a horizontal force F = mg on particle B as shown in figure. Then:
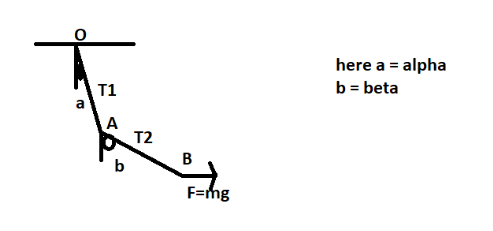
${\text{A}}{\text{. tan}}\beta {\text{ = 2tan}}\alpha $
${\text{B}}{\text{. 2}}{{\text{T}}_1} = 5{{\text{T}}_2}$
${\text{C}}{\text{. }}\sqrt 2 {{\text{T}}_1} = \sqrt 5 {{\text{T}}_2}$
${\text{D}}{\text{.}}$ None of these

Answer
617.1k+ views
Hint: At first draw a free body diagram for particles A and B and then resolve the forces into their components along X- axis and Y- axis.
Formula used - ${T_1}\sin \alpha = {T_2}\sin \beta $ , ${T_1}\cos \alpha = {T_2}\cos \beta + mg$ , ${T_2}\cos \beta = mg$ , ${T_2}\sin \beta = mg$
Complete Step-by-Step solution:
Let us first draw the free body diagram (FBD) for both the particles A and B.
Refer the image shown (FBD)-
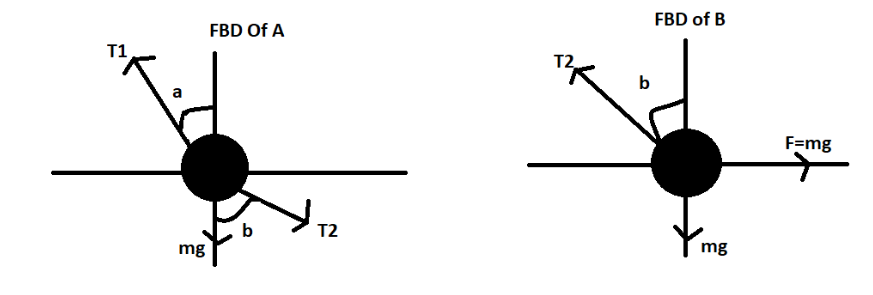
Here $a = \alpha ,b = \beta $ .
Now resolving these forces into their components along X- axis and Y- axis, we get-
From the FBD of A,
${T_1}\sin \alpha = {T_2}\sin \beta - (1)$
${T_1}\cos \alpha = {T_2}\cos \beta + mg - (2)$
Now from the FBD of B,
${T_2}\cos \beta = mg - (3)$
${T_2}\sin \beta = mg - (4)$
now dividing equation 4 by equation 3 we get-
$\dfrac{{{T_2}\sin \beta }}{{{T_2}\cos \beta }} = \dfrac{{mg}}{{mg}}$
So, we get- $\tan \beta = 1$
Using equation (4) in (1) and equation (3) in (2),
$T\sin \alpha = mg$ and $T\cos \alpha = 2mg$
So, dividing these two we get-
$\tan \alpha = \dfrac{1}{2}$
We can also write,
$
2\tan \alpha = 1 \\
\Rightarrow 2\tan \alpha = \tan \beta \{ \because \tan \beta = 1\} \\
$
It means option A is correct.
Now using $\alpha $ and $\beta $ values in (1) we get-
${T_1}\sin \alpha = {T_2}\sin \beta $
$\sqrt 2 {{\text{T}}_1} = \sqrt 5 {{\text{T}}_2}$ (option C)
Therefore, options A and C are correct.
Note – Whenever such types of questions appear then always write the things given in the question and then by drawing the FBD of A and B solve the question, as done in the solution, the forces are resolved into components and then we have found the correct options by using the equations mentioned in the solution.
Formula used - ${T_1}\sin \alpha = {T_2}\sin \beta $ , ${T_1}\cos \alpha = {T_2}\cos \beta + mg$ , ${T_2}\cos \beta = mg$ , ${T_2}\sin \beta = mg$
Complete Step-by-Step solution:
Let us first draw the free body diagram (FBD) for both the particles A and B.
Refer the image shown (FBD)-
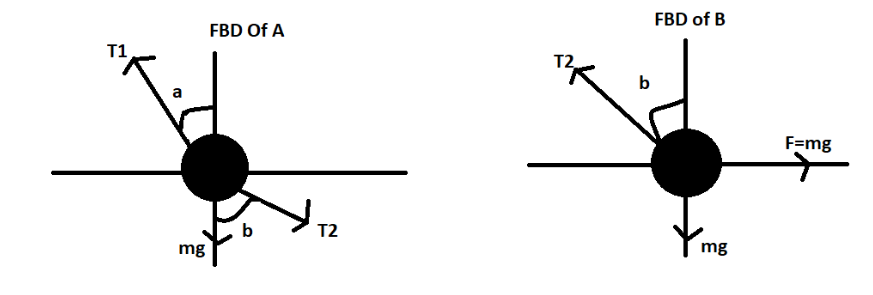
Here $a = \alpha ,b = \beta $ .
Now resolving these forces into their components along X- axis and Y- axis, we get-
From the FBD of A,
${T_1}\sin \alpha = {T_2}\sin \beta - (1)$
${T_1}\cos \alpha = {T_2}\cos \beta + mg - (2)$
Now from the FBD of B,
${T_2}\cos \beta = mg - (3)$
${T_2}\sin \beta = mg - (4)$
now dividing equation 4 by equation 3 we get-
$\dfrac{{{T_2}\sin \beta }}{{{T_2}\cos \beta }} = \dfrac{{mg}}{{mg}}$
So, we get- $\tan \beta = 1$
Using equation (4) in (1) and equation (3) in (2),
$T\sin \alpha = mg$ and $T\cos \alpha = 2mg$
So, dividing these two we get-
$\tan \alpha = \dfrac{1}{2}$
We can also write,
$
2\tan \alpha = 1 \\
\Rightarrow 2\tan \alpha = \tan \beta \{ \because \tan \beta = 1\} \\
$
It means option A is correct.
Now using $\alpha $ and $\beta $ values in (1) we get-
${T_1}\sin \alpha = {T_2}\sin \beta $
$\sqrt 2 {{\text{T}}_1} = \sqrt 5 {{\text{T}}_2}$ (option C)
Therefore, options A and C are correct.
Note – Whenever such types of questions appear then always write the things given in the question and then by drawing the FBD of A and B solve the question, as done in the solution, the forces are resolved into components and then we have found the correct options by using the equations mentioned in the solution.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Which are the three major ports of Tamil Nadu A Chennai class 10 social science CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Describe the process of Unification of Italy class 10 social science CBSE




