Question

Two parabolas have the same axis and tangents are drawn to the second from points on the first; prove that the locus of the middle points of the chords of contact with the second parabola all lie on a fixed parabola.

Answer 1

Hint: Draw tangents from the outer parabola to the inner. Check where the tangents touch the inner parabola and find the midpoint of these points.

Complete step-by-step answer:

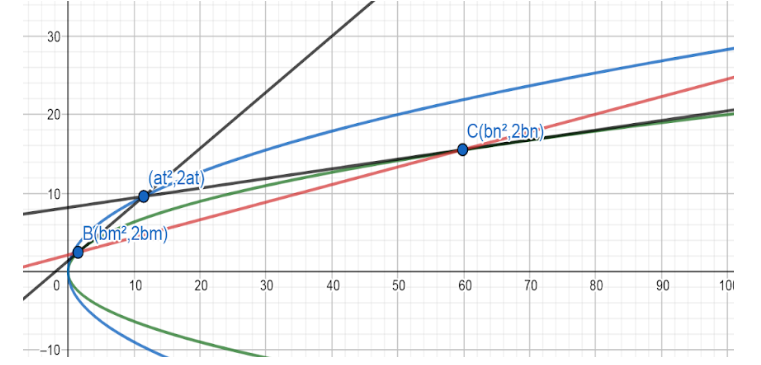
Consider the above picture.
There are two parabolas blue\[\left( {{y}^{2}}=4ax \right)\]and green\[\left( {{y}^{2}}=4bx \right)\]
From point \[A\] (parameter \[t\]) on the blue parabola, two black tangents to the green parabola are drawn. These tangents touch the green parabola at points \[B\] (parameter \[m\]) and \[C\] (parameter \[n\]).
We have to find the locus of mid points of the chord \[BC\].
Since \[AB\] and \[AC\] are tangents to the green parabola, we can write their equations using the parametric form of tangent which is \[ty=x+a{{t}^{2}}\], where \[t\] is the parameter of the point where it touches the parabola.
So we write equations of \[AB\] and \[AC\],
\[AB:my=x+b{{m}^{2}}...(i)\]
\[AC:ny=x+b{{n}^{2}}...(ii)\]
Since these two lines intersect at \[A\], by solving the above equations together we will get point \[A\].
Subtracting equation \[(i)\] from \[(ii)\]i.e. \[\left( ii \right)-\left( i \right)\] we get,
\[\left( ny \right)-\left( my \right)=\left( x+b{{n}^{2}} \right)-\left( x+b{{m}^{2}} \right)\]
\[ny-my=b{{n}^{2}}-b{{m}^{2}}\]
\[y(n-m)=b({{n}^{2}}-{{m}^{2}})\]
\[y(n-m)=b(n-m)(n+m)\]
\[y=b(n+m)...(iii)\]
Substituting equation \[\left( iii \right)\] in \[\left( i \right)\]we get,
\[n(b(n+m))=x+b{{n}^{2}}\]
\[bn(n+m)=x+b{{n}^{2}}\]
\[b{{n}^{2}}+bnm=x+b{{n}^{2}}\]
\[bnm=x\]
\[A:\left( bmn,b\left( m+n \right) \right)\]
Also\[A\] lies on the green parabola, so it must satisfy its equation i.e. \[\left( {{y}^{2}}=4ax \right)\].
So,
${{\left( b\left( m+n \right) \right)}^{2}}=4a\left( bmn \right)...(iv)$
To find the locus of a point, we consider a point with coordinates\[\left( h,k \right)\], which is a general point on the locus.
Since \[\left( h,k \right)\]lies on the locus which is the locus of midpoints of the chord of the parabola.
Using midpoint formula we can write,
Xmid=\[\dfrac{x1+x2}{2}\]
ymid= \[\dfrac{y1+y2}{2}\]
Therefore,
$h=\left\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\}$
$k=\left\{ \dfrac{\left( y~coordinate~of~A \right)+\left( y~coordinate~of~B \right)}{2} \right\}$
$h=\left\{ \dfrac{\left( \text{b}{{\text{m}}^{2}} \right)+\left( b{{n}^{2}} \right)}{2} \right\}$
$2h=\left( \text{b}{{\text{m}}^{2}} \right)+\left( b{{n}^{2}} \right)$
$\dfrac{2h}{b}=\left\{ {{\text{m}}^{2}}+{{n}^{2}} \right\}...(v)$
$k=\left\{ \dfrac{\left( 2bm \right)+\left( 2bn \right)}{2} \right\}$
$k=bm+bn$
$\dfrac{k}{b}=\left\{ m+n \right\}...(vi)$
So our next task in finding the locus is eliminating the variables from the above equations.
Squaring equation\[\left( vi \right)\]and subtracting it from \[\left( v \right)\] i.e. \[{{\left( vi \right)}^{2}}-\left( v \right)\]
Which gives,
${{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}={{\left( m+n \right)}^{2}}-\left\{ {{\text{m}}^{2}}+{{n}^{2}} \right\}$
${{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}=\left( {{m}^{2}}+{{n}^{2}}+2mn \right)-\left\{ {{\text{m}}^{2}}+{{n}^{2}} \right\}$
${{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}=2mn...(vii)$
Substituting equations \[\left( vi \right),\text{ }\left( vii \right)\] in \[\left( iv \right)\]we get,
${{\left( b\left( \dfrac{k}{b} \right) \right)}^{2}}=2ab\left( {{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b} \right)$
${{\left( k \right)}^{2}}=2ab\left( \left( \dfrac{{{k}^{2}}}{{{b}^{2}}} \right)-\dfrac{2h}{b} \right)$
${{\left( k \right)}^{2}}=\left( \left( 2a\dfrac{{{k}^{2}}}{b} \right)-8ah \right)$
${{k}^{2}}=2a\dfrac{{{k}^{2}}}{b}-8ah$
This is the required locus.
Now since \[\left( h,k \right)\]are general points on our locus we can replace \[h\] by \[x\] and \[k\] by \[y\].
$\left( \dfrac{2a}{b}-1 \right){{y}^{2}}=8ax$
This is the required locus which represents another parabola.

Note: Students have to think carefully while deciding which is the variable before eliminating. In this question students might eliminate \[a\] which will give them the wrong answer. Also they may use their different techniques to eliminate the variable from the equations. Also, if they feel it is redundant to use \[\left( h,k \right)\] first and then replace it as \[\left( x,y \right)\] they may use \[\left( x,y \right)\] from the start as well.