Question

Two objects of masses 100g and 200g are moving along the same line and direction with velocities $2m{s^{ - 1}}$ and $1m{s^{ - 1}}$ respectively. They collide and after the collision, the second object moves with a velocity of $1.67m{s^{ - 1}}$. Determine the velocity of the first object:
A) $0.66m{s^{ - 1}}$
B) $0.55m{s^{ - 1}}$
C) $1.66m{s^{ - 1}}$
D) $0.33m{s^{ - 1}}$

Answer 1

Hint: Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing a change in motion of bodies. Collision is of three types:
(i) Perfectly elastic collision.
(ii) Inelastic collision.
(iii) Perfectly inelastic collision.
To solve this type of question we use the law of conservation of momentum.

Complete step by step answer:
Given, ${m_1} = 100g,{m_2} = 200g,{u_1} = 2m/s,{u_2} = 1m/s,{v_2} = 1.67m/s$
We have to find the velocity of the first object $v_1$.
Flowing is the diagram showing the situation.

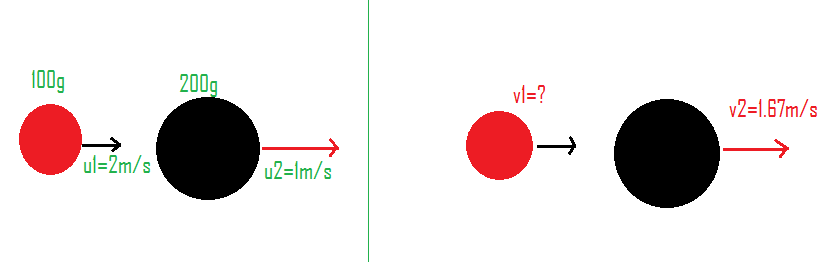
Now let us use the concept of conservation of linear momentum which states that the total initial momentum is equal to the total final momentum.
Initial momentum = Final momentum
Let us write the linear momentum of the system before the collision.
${P_{initial}} = {m_1}{u_1} + {m_2}{u_2}$
Let us now substitute the values.
$\Rightarrow {P_{initial}} = 0.1 \times 2 + 0.2 \times 1$
Let us simplify it.
$\Rightarrow {P_{initial}} = 0.4kgm/s$ ………...(1)
Let us write the linear momentum of the system after the collision.
$ {P_{final}} = {m_1}{v_1} + {m_2}{v_2}$
Let us now substitute the values.
$\Rightarrow {P_{final}} = 0.1{v_1} + 0.2 \times 1.67$
Let us simplify it.
$\Rightarrow {P_{final}} = 0.1{v_1} + 0.334$ …………..(2)
Now using linear momentum conservation, let us equate equation (1) and (2).
$\Rightarrow 0.4 = 0.1{v_1} + 0.334$
Let us simplify it.
$\Rightarrow 0.4 - 0.334 = 0.2{v_1} \Rightarrow {v_1} = \dfrac{{0.066}}{{0.2}}$
$\Rightarrow {v_1} = 0.33m/s$

$\therefore $ The velocity of the first object is 0.33m/sec. Hence, option (D) correct.

Note:
There are two types of collisions between two bodies as given below:
1) Head-on collisions (also known as one-dimensional collisions) – In this type of collision, the velocity of each body just before impact is along the line of impact after collision also.
2) Non-head-on collisions, (also known as two-dimensional collisions) – In this type of collision, the velocity of each body just before impact is not along the line of impact after the collision.