Question

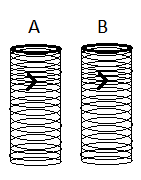
Two metallic rings A and B, identical in shape and size but having different resistivities ${{\rho }_{A}}$ and ${{\rho }_{B}}$, are kept on top of two identical solenoids as shown in the figure. When current I is switched on in both the solenoids in identical manner, the rings A and B jump to heights ${{h}_{A}}$ and ${{h}_{B}}$ respectively, with ${{h}_{A}}>{{h}_{B}}$. The possible relation(s) between their resistivities and their masses ${{m}_{A}}$ and ${{m}_{B}}$ is(are)

$\begin{align}
  & \text{A}\text{. }{{\rho }_{A}}>{{\rho }_{B}}\text{ }and\text{ }{{m}_{A}}={{m}_{B}} \\
 & \text{B}\text{. }{{\rho }_{A}}<{{\rho }_{B}}\text{ }and\text{ }{{m}_{A}}={{m}_{B}} \\
 & \text{C}\text{. }{{\rho }_{A}}>{{\rho }_{B}}\text{ }and\text{ }{{m}_{A}}>{{m}_{B}} \\
 & \text{D}\text{. }{{\rho }_{A}}<{{\rho }_{B}}\text{ }and\text{ }{{m}_{A}}<{{m}_{B}} \\
\end{align}$

Answer 1

Hint: Two identical metallic rigs with same shape and size and different resistivities are placed on two solenoids. It is said when the same current is passed through them both the rings jump at different heights. Since we are not given any information about how close they are kept, we don’t need to consider mutual induction. The only cause of the work done here is the force produced due to the magnetic field. From this we can form the relation between height, resistivity and mass of the two rings.

Formula used:
$W=Fd=mgh$

Complete answer:
In the question we are given two metal rings placed on a solenoid.
It is said that they both have the same shape and size but their resistivities are different.
The resistivity of the ring A is ${{\rho }_{A}}$ and of the ring B is ${{\rho }_{B}}$.
Now a current ‘I’ is passed through both the solenoids in the same manner and due to this the rings A and B jump to heights ${{h}_{A}}$ and ${{h}_{B}}$ respectively.
It is said that, ${{h}_{A}} > {{h}_{B}}$
We know that when a current is passed through a solenoid, it experiences a magnetic field. Add when this current is passed through the metal ring it produces a charge.
Hence we can consider this situation as a charged conductor in a magnetic field.
Therefore we can say that there is a force produced due to this charged conductor in the magnetic field and this causes the metal rings to jump to a height.
This force does a work which is against the magnetic field.
Therefore we can say that,
$W=Fd=mgh$, where ‘F’ is the force, ‘d’ is the displacement, ‘m’ is the mass, ‘g’ is acceleration due to gravity and ‘’ is the height.
$\Rightarrow Fd=mgh$
From this equation, we can say that
$\Rightarrow \dfrac{Fd}{m}=hg$
We know that in this case displacement and acceleration due to gravity are constants .
Therefore,
$\Rightarrow h\propto \dfrac{1}{m}$
$\Rightarrow h\propto F$
Here the height is inversely proportional to mass and directly proportional to force.
In this case the force produced due to the magnetic field depends on the current in the system. We know that the current passed through them is the same, hence current is also constant.
We know that,
\[I=\dfrac{V}{R}\], i.e. current is inversely proportional to resistance.
Since we know that resistance and resistivity are directly proportional, we can say that height is also inversely proportional to resistivity.
Since ${{h}_{A}}>{{h}_{B}}$, for ${{h}_{A}}$ to increase,
 ${{h}_{A}}\propto \dfrac{1}{{{\rho }_{A}}}$ and ${{h}_{A}}\propto \dfrac{1}{{{m}_{A}}}$
Therefore we can say that,
${{\rho }_{A}}<{{\rho }_{B}}$ and \[{{m}_{A}}<{{m}_{B}}\]

So, the correct answer is “Option D”.

Note:
Here when we pass current through it the magnetic field changes and eddy current is formed inside the solenoid. Eddy currents are simply loops of electrical current which is induced inside the conductor when we apply an alternating magnetic field to the conductor. This inducing of current occurs according to Faraday’s laws of induction.