Question

Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are connected by a string of length L. They are held in horizontal plane at height H above two fixed heavy plates A and B made of different material placed on floor. Initially distance between two masses is a < L. When the masses are released, they make collisions with A and B with coefficients of restitution 0.8 and 0.4 respectively. The time after collision after string becomes tight is:

        

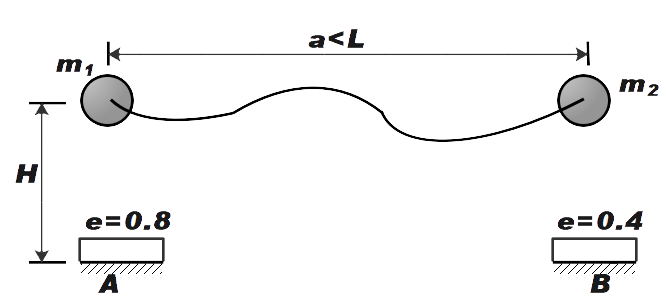
A. \[\dfrac{5}{2}\sqrt{\dfrac{{{L}^{2}}-{{a}^{2}}}{2gH}}\]
B. \[\sqrt{\dfrac{2g}{H}}\]
C. \[\dfrac{3}{2}\sqrt{\dfrac{{{L}^{2}}-{{a}^{2}}}{2gH}}\]
D. none of the above

Answer 1

Hint: In this question we have been asked to calculate the time after collision when the string will become tight. We know that both the masses after collision will have different velocity and will therefore gain different speeds vertically upwards after collision. This will stretch the string completely i.e. a = L. Therefore, we have to find time required for the same. We shall be using the equation of motion as we are dealing with the gravity, speed of particles and time.

Formula used:
 \[s=ut+\dfrac{1}{2}{{t}^{2}}\]

Complete answer:
To solve this question,
Let us assume that the mass \[{{m}_{1}}\] attains a height \[{{h}_{1}}\] after collision and \[{{m}_{2}}\] attains height \[{{h}_{2}}\] as shown in the figure below.

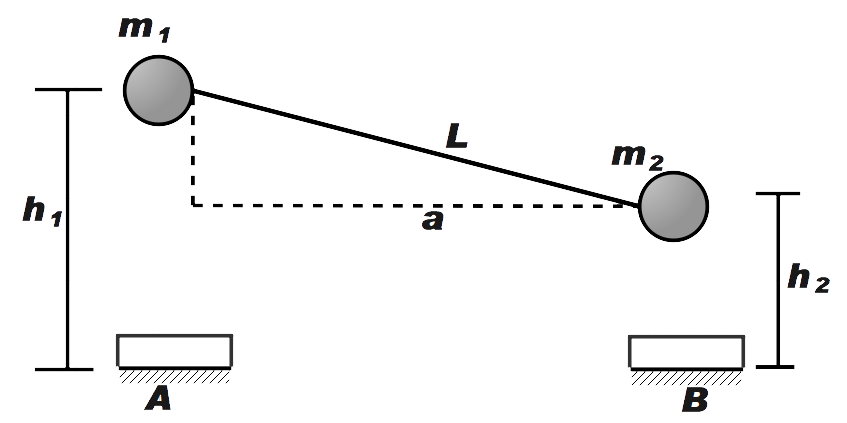
Now, we know that coefficient of restitution is given as ratio of final to initial velocity between two objects after they collide.
Therefore, we can say that
Velocity of mass \[{{m}_{1}}\] is given by \[0.8v\]and mass \[{{m}_{2}}\] is given by \[0.4v\]
Therefore, we can now say that \[{{m}_{1}}\] and \[{{m}_{2}}\] will attain height as shown in the figure.
Now from the figure,
We can say that
\[{{h}_{1}}-{{h}_{2}}=\sqrt{{{L}^{2}}-{{a}^{2}}}\] …………… (Pythagoras theorem) …………. (1)
From equation of motion
\[s=ut+\dfrac{1}{2}{{t}^{2}}\]
For mass \[{{m}_{1}}\], we know that s = \[{{h}_{1}}\], u = 0.8v
Therefore,
We get,
\[{{h}_{1}}=0.8v\times t-\dfrac{1}{2}g{{t}^{2}}\] ……………. (2)
Similarly, for mass \[{{m}_{2}}\]
We get,
\[{{h}_{2}}=0.4v\times t-\dfrac{1}{2}g{{t}^{2}}\] ……………….. (3)
Now from (1), (2) and (3)
We get,
\[\sqrt{{{L}^{2}}-{{a}^{2}}}=0.4v\times t\]
Therefore, solving for time
 We get,
\[t=\dfrac{\sqrt{{{L}^{2}}-{{a}^{2}}}}{0.4v}\]
Now, from potential energy theorem,
We know that
\[v=\sqrt{2gH}\]
Also, we can say that,
\[0.4=\dfrac{4}{10}=\dfrac{2}{5}\]
Therefore,
We can say that,
\[t=\dfrac{5}{2}\sqrt{\dfrac{{{L}^{2}}-{{a}^{2}}}{2gH}}\]

So, the correct answer is “Option A”.

Note:
Coefficient of restitution usually denoted by e determines whether a collision is elastic or inelastic in nature. During a collision, after the collision the kinetic energy would get transferred to the other object. The coefficient of restitution largely depends on the material of the surface or solid on which the object collides. It also depends on the shape and size of the colliding particle as well as impact velocity.