Question

Two lines perpendicular to the same line are perpendicular to each other.
A. True
B. False

Answer 1

Hint: First, we have to change the question to a diagram model for our understanding. Then by proving that the corresponding angles are equal it can be checked whether those two lines perpendicular to the same line are perpendicular to each other.

Complete step-by-step answer:
Let $PQ$ and $RS$ be two lines which is perpendicular to same line $MN$
               

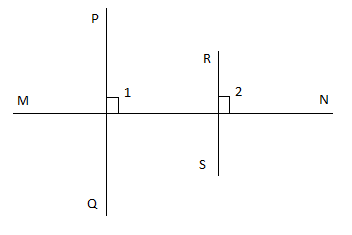
From the above diagram, it is clear that \[PQ \bot MN\] and $RS \bot MN$.
Therefore, the angle formed by $PQ$ on $MN$, which is taken as $\angle 1 = 90_{}^0$
And the angle formed by $RS$ on $MN$, which is taken as $\angle 2 = 90_{}^0$
So, $\angle 1 = \angle 2$
Thus we can say that both these lines $PQ$ and $RS$ form equal corresponding angles
∴ \[PQ\parallel RS\]
Hence it is proved that $PQ$ and $RS$ are not perpendicular to each other.

So, the correct answer is “Option B”.

Note: Perpendicular lines are those lines which intersect each other at right angles, that is, \[90_{}^0\]. It is to be noted that when you multiply the slopes of perpendicular lines in a plane you will get \[ - 1\] which means the slope of perpendicular lines are opposite reciprocals.
Parallel lines are those lines which will never intersect each other. Parallel lines have huge application in practical life. It has wide application in the construction industry. There are many examples of parallel lines in real life which include road tracks, edges of sidewalk and many more. The name given to angles formed by parallel lines are alternate interior angles, alternate exterior angles, corresponding angles, and interior angles on the same side of the transversal.