Question

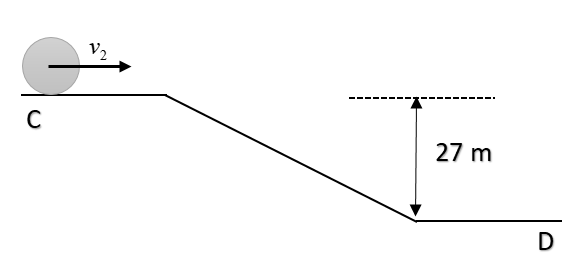
Two identical uniform discs roll without slipping on two different surfaces AB and CD starting A and C with linear speed $v_1 \ and \ v_2$ respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed and $v_1 = 3m/s$, then$v_2 \ in \ m/s \ is \ (g = 10m/s^2$):

Answer 1

Hint: Kinetic energy is the energy possessed in the body due to its motion. There are two types of kinetic energies: Transitional and rotational kinetic energy. When a body just translates or simply moves, it possesses only translational kinetic energy. But when the body both translates and rotates, it possesses translational and rotational kinetic energies. This is also called rolling of a body. Use this concept and apply expression for rotational and translational kinetic energy. Establish the initial and final value of kinetic energy of the uniform disc, then apply work energy theorem to the obtained values. Later simplify for the required answer.

Formula used:
$K.E = \dfrac12 mv^2 + \dfrac12 I\omega^2$

Complete step-by-step answer:
Here we are given a rolling disc which undergoes decrease in elevation from point A to B and from point C to D. Since the disc will always remain in contact with the surface and there is no slipping, thus we have to concentrate on kinetic energy and potential energy only.
Now, we know that the kinetic energy of any rolling object is given by$K.E. = \dfrac12 mv^2 + \dfrac12 I\omega^2$.
Also, for disc, $I = \dfrac12 mR^2$ and $\omega = \dfrac vR$, thus;
$\dfrac12 I\omega^2 = \dfrac12 \left(\dfrac12 mR^2 \times (\dfrac vR)^2\right) = \dfrac14 mv^2$
Hence $K.E. = \dfrac12 mv^2+ \dfrac14 mv^2 = \dfrac34 mv^2$
Also, by work energy theorem, we can write: $\Delta \ K.E = Work \ done$
Hence $K.E_f - K.E_i = mgh$
Applying for AB, we get;
$\dfrac 34 mv_B^2 - \dfrac34mv_1^2 = mgh$
$v_B^2 = v_1^2 + \dfrac43gh$
Putting the values, we get;
$v_B = \sqrt{v_1^2+40g}$

Now, applying for CD, we get;
$\dfrac34 mv_D^2 - \dfrac34mv_2^2 = mgh\prime$
$v_D^2 = v_2^2 + \dfrac43gh\prime$
Putting the values, we get;
$v_D = \sqrt{v_2^2+36g}$
Since, it is given that$v_B = v_D$, hence;
$\sqrt{v_1^2+40g} = \sqrt{v_2^2+36g}$
$\therefore v_2 = \sqrt{v_1^2 + 4g}$
As $v_1 = 3m/s$
Thus $v_2 = \sqrt{3^2 + 4\times 10} = \sqrt{49} m/s$
So $v_2 = 7 m/s$

Note: When a body is rolling, it has two types of kinetic energy, transitional as well as rotational. Chance of mistake is higher that a student will forget to write additional rotational energy. So a student should always think while writing the kinetic energy equation. Also, the angular velocity of any object under pure translation is zero. Also the moment of inertia in the equation of kinetic energy is taken about the axis of rotation, which is centre in this case. But it is not always centre, it could be any general point.