Question

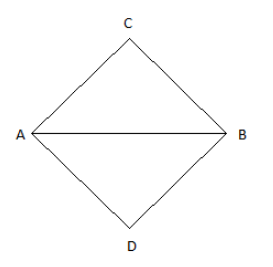
Two identical rectangular rods of metal are welded end to end in series between temperature \[{0^ \circ }C\] and \[{100^ \circ }C\] 10J of heat is conducted (in the steady-state process) through the rod in 2.00 min. If 5 such rods are taken and joined as shown in figure maintaining the same temperature difference between A and B.
(A) The time in which 20J heat will flow through the rods is 30 sec.
(B) The time in which 20J heat will flow through the rods is 60 sec.
(C) The net rate of heat transfer through the new structure is \[\dfrac{1}{3}{\text{J/sec}}\]
(D) The net rate of heat transfer through the new structure is \[\dfrac{2}{3}{\text{J/sec}}\].

Answer 1

Hint: In this question, determine the temperature difference between the points A and B such that five similar rods have been joined as shown in the figure. For this, we will use the relation between the heat transfer between the two points and the temperature difference between the same points.

Complete step by step answer:
Given the temperature changes from \[{0^ \circ }C\] to \[{100^ \circ }C\] so, \[\Delta T = {100^ \circ }C\]
Let the cross-sectional area of the rod be A.
We know the heat transfer by conduction is given as, \[Q = \dfrac{{kA}}{l}\left( {{T_1} - {T_2}} \right) - - (i)\]
Here initially two identical rectangular rods of metal is welded, so the length become ‘2l’ and the temperature changes from \[{0^ \circ }C\] to \[{100^ \circ }C\] and 10 joules of heat is conducted for 2 minutes; hence we get
\[
\dfrac{{dQ}}{{dt}} = \dfrac{{kA}}{{2l}}\left( {{T_1} - {T_2}} \right) \\
\Rightarrow\dfrac{{20}}{{120}} = \dfrac{{kA}}{{2l}}\left( {100 - 0} \right) \\
\Rightarrow\dfrac{{kA}}{{2l}}\left( {100} \right) = \dfrac{{20}}{{120}} - - (ii) \\
 \]
Now when 5 rods are welded
Let us assume the rods to be a resistor.

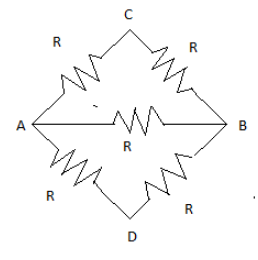
Where Resistances in ACB and ADB are in series hence their net resistances will be 2R respectively, and resistance R between AB is in parallel with resistances in ACB and ADB; hence the total equivalent resistance will be
\[
\Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2R}} + \dfrac{1}{R} + \dfrac{1}{{2R}} \\
\Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{{1 + 2 + 1}}{{2R}} \\
\Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{4}{{2R}} \\
\Rightarrow\dfrac{1}{{{R_{eq}}}} = \dfrac{2}{R} \\
 \]
Therefore the equivalent resistance is \[ = \dfrac{R}{2}\]
Similarly, the thermal conductivity will be

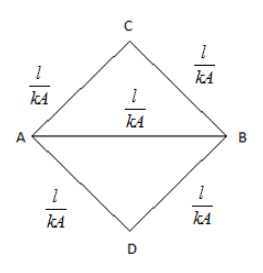
So the equivalent thermal conductivity between AB will be \[\dfrac{l}{{2kA}}\]
Therefore its heat transfer will be
\[
\Rightarrow\dfrac{{dQ}}{{dt}} = \dfrac{1}{{\left( {\dfrac{l}{{2kA}}} \right)}}\left( {{T_1} - {T_2}} \right) \\
\Rightarrow\dfrac{{20}}{x} = \dfrac{{2kA}}{l}\left( {100 - 0} \right) \\
\Rightarrow\dfrac{{20}}{x} = 2 \times 2\left( {\dfrac{{kA}}{{2l}}\left( {100 - 0} \right)} \right) \\
\]
Now since the value of \[\dfrac{{kA}}{{2l}}\left( {100} \right) = \dfrac{{20}}{{120}}\]from equation (ii), we can further write the equation
\[
\Rightarrow\dfrac{{20}}{x} = 2 \times 2 \times \dfrac{{20}}{{120}} \\
\Rightarrow x = \dfrac{{120 \times 20}}{{2 \times 2 \times 20}} \\
\therefore x= 30\sec \\
 \]
Therefore the time in which $20 J$ heat will flow through the rods\[ = 30\sec \].
Hence, option A is correct.

Note:It is interesting to note here that, the equivalent formula for evaluating the thermal conductivity is equivalent to the formula used for calculating the equivalent resistance connected in a series-parallel connection. Moreover, heat transfer by thermal conduction is given by the formula \[Q = \dfrac{{kA}}{l}\left( {{T_1} - {T_2}} \right)\], where Q is the heat transferred, k is the thermal conductivity constant, area of the cross section of material, l is the length of material through which heat is being transferred.