Question

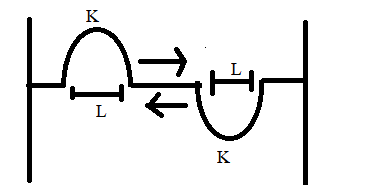
Two identical pulses move in opposite directions with same uniform speeds on a stretched string. The width and kinetic energy of each pulse is L and k respectively. At the instant they completely overlap, the kinetic energy of the width L of the string where they overlap is

A. \[k\]
B. \[2k\]
C. \[4k\]
D. \[8k\]

Answer 1

Hint: The above problem can be resolved by using the principle of superposition of the sound waves. When the sound waves or the pulses of similar velocity or the similar frequency overlap, then the resultant sound wave or the pulse wave that will be formed is two times that of the initial one. And the kinetic energy varies with the square of the velocity. Hence the magnitude of kinetic energy will also change accordingly.

Complete step by step answer:
The mathematical expression for the kinetic energy of the string is given as,
\[KE = \dfrac{1}{2}m{v^2}\] ………………………………….. (1)
Here, m is the pulse string and v is the velocity at which the pulse is travelling.
When there is the overlapping of the pulses, there velocity profiles will also overlap in the context of each other. The velocity profiles of both the pulse is similar and then by applying the principle of superposition, the velocity of the pulse will become twice.
Then from equation 1 as,
\[\begin{array}{l}
K{E_1} = \dfrac{1}{2}m{\left( {2v} \right)^2}\\
K{E_1} = 4\left( {\dfrac{1}{2}m{v^2}} \right)\\
K{E_1} = 4KE
\end{array}\]
Therefore, the kinetic energy of the pulse of string is 4 times that is \[4k\] and option (C) is correct.

Note:To solve the given problem, one must be sure about the mathematical formula of the kinetic energy. To relate these concepts, it is also important to remember the concept of the superimposition of the waves, having variation in the variables like velocity, frequency, amplitude and many more. As this is completely reliable to predict the relation of the variables with the energy associated by the wave.