Question

Two foolhardy daredevil drivers are facing each other at the either end of a straight track. The first accelerates to $16m{{s}^{-1}}$ over 3sec while the second accelerates to $20m{{s}^{-1}}$ over 5sec. They both continue at their speeds and the crash occurs 9sec after they start. How long is the track?

Answer 1

Hint: As a first step, note down all the quantities given the above question. Then you would realize that both the drivers are at rest at the very beginning and hence have zero initial velocity. So, you could find the distances travelled by each of them to reach the point of crash and their sum would be the length of the track.
Formula used:
Equation of motion,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete answer:
In the question, we have two foolhardy daredevil drivers at the two ends of a straight track. Both of their acceleration is given in the question. We are also told that they crash into each other after 9 seconds. We are supposed to find the total length of the track.
Let A be the point at which both of them crash into each other. We could simply find the distance travelled by each of them to reach that point and their sum will give the length of the track.

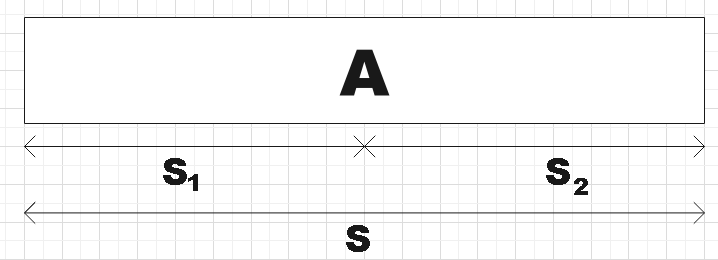
We know that both the drivers are at rest at the beginning and are being accelerated to the acceleration provided in the question. So their accelerations would be: ${{a}_{1}}=\dfrac{16}{3}m{{s}^{-2}}$ and ${{a}_{2}}=\dfrac{20}{5}=4m{{s}^{-2}}$ respectively. Their initial velocities would be, ${{u}_{1}}={{u}_{2}}=0$
The distances travelled by them could be found by,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
For first driver,
${{s}_{1}}=0+\dfrac{1}{2}\times \left( \dfrac{16}{3} \right)\times {{9}^{2}}$
$\Rightarrow {{s}_{1}}=216m$ ……………………………………………….. (1)
For the other driver,
${{s}_{2}}=0+\dfrac{1}{2}\times \left( 4 \right)\times {{9}^{2}}$
$\Rightarrow {{s}_{2}}=162m$ …………………………………………….. (2)
Now, the length of the track would be the sum,
$S={{s}_{1}}+{{s}_{2}}$
$\Rightarrow S=216m+162m$
$\therefore S=378m$
Therefore, we found the length of the track to be 378m.

Note:
We have directly substituted time t=9s while finding the solution. This is because we are finding the distance travelled before crashing and we are said that they take 9s to reach this point of crash but with different velocities. So, we have done the substitution accordingly to find the answer.