Question

Two cross roads, each of width 10m, cut at right angles through the center of a rectangular park of length 700m and breadth 300m and parallel to its sides. Find the area of the roads. Also find the area of the park excluding cross roads. Give the answer in hectares.

Answer 1

Hint:
Here, first we have to find the area of the road, Then, to find the Area of park excluding the cross road we have to subtract Area of park and Area of road.

Complete step by step solution:

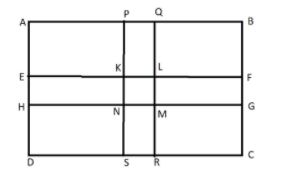
Here we have given that \[PQ = 10m\], \[PS = 300m\], \[EH = 10m\], \[EF = 700m\], \[KL = 10m\]
Area of roads = Area of PQRS + Area of EFGH – Area of KLMN
 $ = PS \times PQ + EF \times EH - KL \times KN$
 $ = \left( {300 \times 10} \right) + \left( {700 \times 10} \right) - \left( {10 \times 10} \right) \\
\Rightarrow 3000+7000-100 \\
 \Rightarrow 9.900{m^2}$
Area of roads in hectors,
 $1{m^2} = \dfrac{1}{{10000}} \text{hectares}$
 $\therefore 9.900{m^2} = \dfrac{{9900}}{{10000}} = 0.99 \, \text{hectares}$
Now,
Area of park excluding cross roads = Area of park – Area of road
 $ = \left( {AB \times AD} \right) - 9900$
 $ = \left( {700 \times 300} \right) - 9900 \\
 =210000-9900 $
 $ = 2,00,100{m^2}$
 $ = \dfrac{{200100}}{{10000}} \text{hectares} \\
 =20.01 hectares$

$\therefore $ The area of the park excluding cross roads is 20.02 hectares.

Note:
Alternate Method:
A and B are two roads in the park.
Area covered by road A
 $ = 700 \times 10{m^2}$
 $ = 7000{m^2}$
Similarly,
Area covered by road B
 $ = 300 \times 10{m^2}$
 $ = 3000{m^2}$
Now,
Common area covered by road A and B
 $ = 10 \times 10{m^2}$
 $ = 100{m^2}$
Area covered by roads
 $ = 7000{m^2} + 3000{m^2} - 100{m^2}$
 $ = 9900{m^2}$
=0.99hectare
 $\therefore $ Area of park
 $ = 700{m^2} \times 300{m^2} = 210000{m^2}$
Area of the park excluding cross road
 $ = 210000{m^2} - 9900{m^2}$
 $ = 200100{m^2}$
=20.01 hectare