Question

Two containers of equal volume contain the same gas at pressures $P_{1}$ and $P_{2}$ and absolute temperatures $T_{1} and T_{2}$ respectively. On joining the vessels, the gas reaches a common pressure $P$ and common temperature $T$. The ratio $\dfrac{P}{T}$ is equal to:
A. $\dfrac{P_1}{T_1} + \dfrac{P_2}{T_2}$
B. $\dfrac{P_1 T_1 \; + P_2 T_2}{(T_1 + T_2)^2}$
C. $\dfrac{ P_1 T_2 \; + P_2 T_1}{(T_1 + T_2)^2}$
D. $\dfrac{P_1}{2T_1} + \dfrac{P_2}{2T_2}$

Answer 1

Hint: Round up all the variables mentioned in the question. Given that you have to deal with a gas, try to come up with some equation of state that relates all these variables to each other, possibly under ideal conditions.

Formula used: Ideal gas equation:
$$PV = nRT$$
Where $P$ is the pressure of the gas, $V$ is the volume occupied, $n$ is the amount of gas, usually mentioned in moles, $R$ is the ideal gas constant ($8.3145 J\;mol^{-1}\;K^{-1}$) and $T$ is the temperature of the gas, all taken in the metrics corresponding to the choice of units in the ideal gas constant.

Complete step by step answer:
Let us assume that the gas in question can be approximated to the behaviour of a hypothetical ideal gas. To this end, we are now authorized to imbibe the ideal gas equation to determine the state of this gaseous system.
  

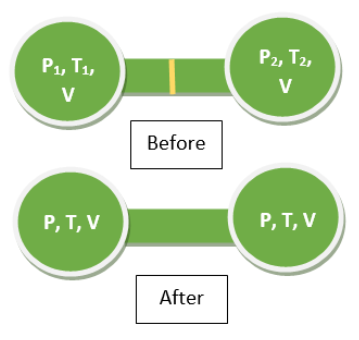
So we first define our variables with respect to the containers as given in the question.
Since both the containers have equal volumes let us take
$$V_1 = V_2 = V$$
Let the gas pressure in the two containers be $P_1$ and $P_2$ respectively and the temperature of the gas in the corresponding containers be $T_1$ and $T_2$.

We now establish the equation of states for both the containers from the ideal gas equation:
$$P_1V = n_1RT_1 \Rightarrow n_1 = \dfrac{P_1V}{RT_1}$$
$$P_2V = n_2RT_2 \Rightarrow n_2 = \dfrac{P_2V}{RT_2}$$

On joining both the vessels, we are combining the volumes of the two vessels, so we get the volume to now be equal to $V + V = 2V$. Let the common pressure and temperature be $P$ and $T$ respectively, and the total amount of gas present be $n_{after}$. The ideal gas equation for this final state becomes:
$$P(2V) = n_{after}RT \Rightarrow n_{after} = \dfrac{P(2V)}{RT}$$
Combining the gas from both the vessels also means that the total amount of substance present in the system will be equal to
$$n_{after} = n_1 + n_2$$
$$\Rightarrow \dfrac{P(2V)}{RT} = \dfrac{P_1V}{RT_1} + \dfrac{P_2V}{RT_2}$$
$$\Rightarrow \dfrac{2P}{T} = \dfrac{P_1}{T_1} + \dfrac{P_2}{T_2} $$
$$\Rightarrow \dfrac{P}{T} = \dfrac{P_1}{2T_1} + \dfrac{P_2}{2T_2} $$

So, the correct answer is “Option D”.

Note: The ideal gas equation is a stoichiometric tool that is used to only approximate the real world behaviour of a gas by extrapolating it to that of an ideal gas. This equation in no way is a means to measure the state variables of a system accurately.
However, this law is the basis of the empirical laws that can be derived to determine the state of a system by keeping two of the variables constant. This paves the way to some of the equations such as Charles’ Law, Boyle’s Law, Avogadro’s Law and Gay-Lussac’s Law that we use extensively in the study of gaseous processes.
Also remember to maintain consistency in the system of units of the quantities used in the ideal gas law, especially for numerical problems.