Question

Two concentric circles are of radius 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer 1

Hint: ${{C}_{1}}$ as the circle with radius 3 cm and ${{C}_{2}}$ as the circle with radius 5 cm. Let us assume O to be the center of the circles. Let the chord of ${{C}_{2}}$ that touches ${{C}_{1}}$ be BD. We will denote the point of contact as C. We can write \[OC=3\text{ cm},OB=OD=5\text{ cm}\] . We have to find BD. We know that tangent at any point of a circle is perpendicular to the radius through the point of contact. Hence, we can write $OC\bot BD$ . Let us consider triangle OBC and OCD and find the side BC and CD respectively using Pythagoras theorem which is given as $\text{Hypotenus}{{\text{e}}^{2}}=\text{Heigh}{{\text{t}}^{2}}+\text{Bas}{{\text{e}}^{2}}$ . Then add BC and CD to get BD which is the required answer.

Complete step-by-step answer:
We are given that two concentric circles are of radius 5 cm and 3 cm. Let us denote ${{C}_{1}}$ as the circle with radius 3 cm and ${{C}_{2}}$ as the circle with radius 5 cm. Let us assume O to be the center of the circles. Let the chord of ${{C}_{2}}$ that touches ${{C}_{1}}$ be BD. We will denote the point of contact as C. This is shown below.

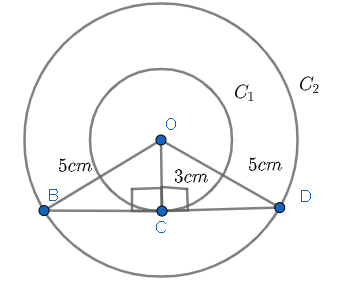
From the figure, we can write \[OC=3\text{ cm},OB=OD=5\text{ cm}\] . We have to find BD.
We know that tangent at any point of a circle is perpendicular to the radius through the point of contact. Hence, we can write $OC\bot BD$ .
Now, let us consider triangle OBC. Since $\angle OCB={{90}^{\circ }}$ , we can use the Pythagoras theorem to find BC.
We know that, $\text{Hypotenus}{{\text{e}}^{2}}=\text{Heigh}{{\text{t}}^{2}}+\text{Bas}{{\text{e}}^{2}}$
$\Rightarrow O{{B}^{2}}=O{{C}^{2}}+B{{C}^{2}}$
Let us substitute the values. We will get
$\begin{align}
  & {{5}^{2}}={{3}^{2}}+B{{C}^{2}} \\
 & \Rightarrow 25=9+B{{C}^{2}} \\
\end{align}$
 Let us find BC.
$\begin{align}
  & \Rightarrow 25-9=B{{C}^{2}} \\
 & \Rightarrow B{{C}^{2}}=16 \\
\end{align}$
Let us take the square root. We will get
$BC=\sqrt{16}=4\text{ cm}$
Similarly, we can find CD.
Let us consider triangle OCD. We found that $\angle OCD={{90}^{\circ }}$ . Thus,
$\Rightarrow O{{D}^{2}}=O{{C}^{2}}+C{{D}^{2}}$
Let us substitute the values. We will get
$\begin{align}
  & {{5}^{2}}={{3}^{2}}+C{{D}^{2}} \\
 & \Rightarrow 25=9+C{{D}^{2}} \\
\end{align}$
 Let us find CD.
$\begin{align}
  & \Rightarrow 25-9=C{{D}^{2}} \\
 & \Rightarrow C{{D}^{2}}=16 \\
\end{align}$
Let us take the square root. We will get
$CD=\sqrt{16}=4\text{ cm}$
Hence, we can write the length of the cord BD as
$BD=BC+CD=4+4=8\text{ cm}$
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.

Note: You have to draw diagrams with given data in order to solve the problems of this type. We can apply Pythagoras theorem in a triangle only when one the angles of the triangle is ${{90}^{\circ }}$ . Do not make mistake by writing Pythagoras theorem as $\text{Hypotenus}{{\text{e}}^{2}}=\text{Heigh}{{\text{t}}^{2}}-\text{Bas}{{\text{e}}^{2}}$ . Also, be careful with the units. Do not forget to write them at the end. You must know the theorems associated with circles to move forward with the solution.