Question

Two climbers are at points \[A\] and \[B\] on a vertical cliff face. To an observer \[C\], 40m from the foot of the cliff, on the level ground. \[A\] is at an elevation \[{48^0}\] and \[B\] of \[{57^0}\]. What is the distance between the climbers?

Answer 1

Hint: In this question, let’s first draw the diagram as mentioned in the question. And using trigonometric ratios, we’ll calculate the side BD. With the value of BD we can calculate the $h$.

Complete step-by-step answer:

Let point \[D\] be the foot of the cliff. And the distance between the climbers i.e., \[AB = h\].
Draw the diagram with \[CD = 40m\] and \[A\] is at an elevation of \[{48^0}\] and \[B\]of \[{57^0}\].

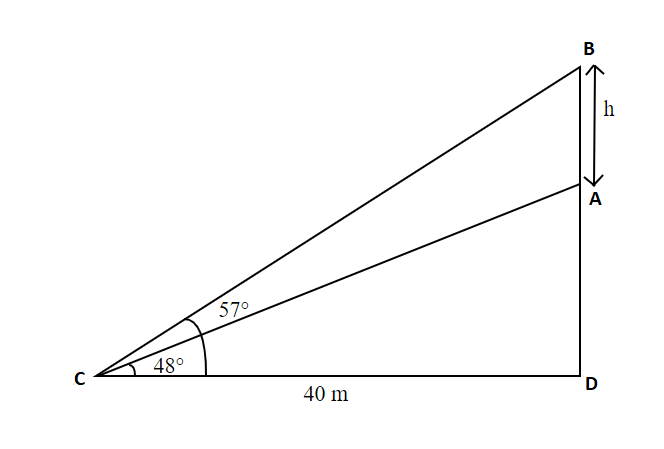
In \[\Delta ACD\],
\[
   \Rightarrow \tan {48^0} = \dfrac{{AD}}{{40}} \\
  \therefore AD = 40\tan {48^0}........................................\left( 1 \right) \\
\]
In \[\Delta BCD\],
\[
   \Rightarrow \tan {57^0} = \dfrac{{DB}}{{40}} \\
   \Rightarrow \tan {57^0} = \dfrac{{AB + AD}}{{40}} \\
   \Rightarrow \tan {57^0} = \dfrac{{h + AD}}{{40}} \\
   \Rightarrow 40\tan {57^0} = h + AD \\
  \therefore AD = 40\tan {57^0} - h...........................................\left( 2 \right) \\
\]

From equations (1) and (2), we have
\[
   \Rightarrow 40\tan {48^0} = 40\tan {57^0} - h \\
   \Rightarrow h = 40\tan {57^0} - 40\tan {48^0} \\
   \Rightarrow h = 40\left( {\tan {{57}^0} - \tan {{48}^0}} \right) \\
   \Rightarrow h = 40\left( {1.539864 - 1.110612} \right) \\
   \Rightarrow h = 40\left( {0.429252} \right) \\
   \Rightarrow h = 17.17008 \\
  \therefore h \cong 17.17m \\
\]

Thus, the distance between the climbers is $17.17m$

Note: Be cautious while drawing the diagram. There will be confusion while writing the angles of elevations, and if it is represented wrong, there will be changes in calculations which leads to wrong answers.