Question

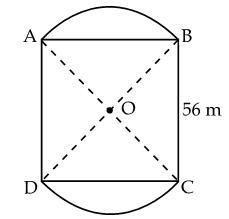
Two circular flower beds have been placed on two side of square lawn ABCD of side 56m. If the centre of each flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and flower beds.

Answer 1

Hint: We use the formula of Area of sector of the circle and the area of square to determine the required. Area of the sector of the circle \[=\left( \dfrac{\pi \theta }{360}-sin\dfrac{\theta }{2}cos\dfrac{\theta }{2} \right){{(r)}^{2}}\], where r is the radius of the sector of the circle, \[\theta \]is the angle subtended by the sector of the circle at the centre. Area of the square is side square.

Complete step-by-step answer:

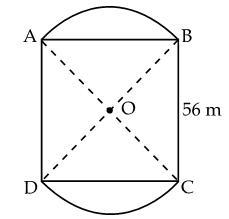
Given two circular flower beds have been placed on two side of square lawn ABCD of side 56m, that is the length AB=BC=AD=CD=56m. Now the centre of each flower bed is the point of intersection O of the diagonals of the square lawn.
We have to determine the sum of areas of the lawn and the flower bed.
Because ABCD is a square so \[\angle A=\angle B=\angle C=\angle D={{90}^{\circ }}\], therefore \[\vartriangle ABC\]is a right-angled triangle. Applying Pythagoras theorem in triangle\[ABC\] we get,

\[\Rightarrow A{{C}^{2}}={{56}^{2}}+{{56}^{2}}\]
Since each side of square measures 56m
\[\Rightarrow A{{C}^{{}}}=56\sqrt{2}m\]
Now, we know that the diagonals of a square bisect each other at \[{{90}^{\circ }}\]then
\[AO=OC\],\[BO=OD\]and \[\angle AOB={{90}^{\circ }}\]
This gives \[AC=AO+OC=2AO\]
Substituting value of\[A{{C}^{{}}}=56\sqrt{2}\], we get
\[AO=\dfrac{56\sqrt{2}}{2}=28\sqrt{2}m\].
Hence, we get the radius of the flower bed or of the circular arc as length of AO which is \[28\sqrt{2}\]m.

Now we have to determine the area of the flower bed. Since the shape of the flower bed is in the form of sector of a circle, so the Area of the flower bed becomes equal to the Area of the sector of the circle which is given by,

Area of the sector of the circle\[=\left( \dfrac{\pi \theta }{360}-sin\dfrac{\theta }{2}cos\dfrac{\theta }{2} \right){{(r)}^{2}}\], where r is the radius of the sector of the circle, here it is equal to AO which is \[28\sqrt{2}\]m, \[\theta \]is the angle subtended by the sector of the circle at the centre here it is \[\angle AOB={{90}^{\circ }}\]
Substituting all the values in above expression, we get
Area of the sector of the circle\[=\left( \dfrac{(22)90}{(7)360}-sin\dfrac{90}{2}cos\dfrac{90}{2} \right){{(28\sqrt{2})}^{2}}\]
\[\Rightarrow \]Area of the sector of the circle \[=\left( \dfrac{(22)90}{(7)360}-sin(45)cos(45) \right){{(28\sqrt{2})}^{2}}\]
\[\Rightarrow \]Area of the sector of the circle \[=\left( \dfrac{11}{14}-\dfrac{1}{2} \right)(28)(28)(2)\].

Then, Area of the flower bed = Area of the sector of the circle\[=448{{m}^{2}}\]

Since there are two flower beds having same area then Area of both the flower bed = 2 times area of one flower bed = (2)(448)= 896\[{{m}^{2}}\]…….(i)
Now we find the area of the square lawn which is equal to the area of the square ABCD.
Thus, area of the square lawn = (56) (56) =3136\[{{m}^{2}}\]………. (ii)

Then the sum of the areas of the lawn and flower beds = equation (i)+ equation (ii)
The sum of the areas of the lawn and flower beds = 896 + 3136= 4032\[{{m}^{2}}\], which is the required result.

Note: The possibility of mistake could be only taking the area of one flower bed in consideration which is wrong, because it is given in the question to obtain the area of both the flower beds. So it is necessary to multiply by 2 to the area obtained from one flower bed.