Question

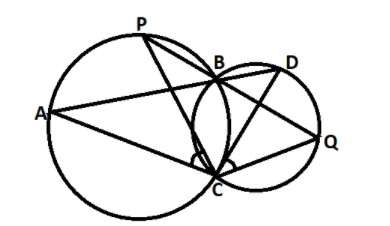
Two circles intersect at two points B and C. Through B, two-line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see figure). Prove that \[\angle ACP = \angle QCD\]

Answer 1

Hint: In this particular question first apply the general identity of the circle that the angles drawn in the same segment of a circle are always equal and then apply the identity of lines that when two lines intersect then the vertically opposite angles made by them are always equal. So, use these concepts to prove the result.

Complete step-by-step answer:
Let us first draw a circle to understand the identity of the circle.

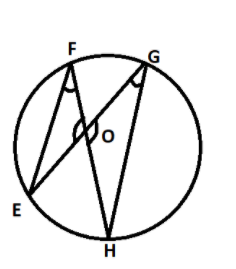
Now in the above circle \[\angle EFH = \angle EGH\] because according to the identity of circle angles drawn from the same segment is always equal.
And \[\angle EFH\] and \[\angle EGH\] are drawn on the same segment EFGHE.
According to the property of vertically opposite angles when two lines intersect each other at a fixed point then the vertically opposite angles to that point are always equal.
So, \[\angle EOF = \angle HOG\] because the lines EOH and GOE intersect each other at O. So, the \[\angle EOF\] and \[\angle HOG\] are vertically opposite angles.
Now let us come to the given figure in the question.
As we can see from the given figure that \[\angle ABP\] and \[\angle ACP\] lie on the same segment PBCAP of the circle.
So, \[\angle ABP = \angle ACP\] (1)
And, \[\angle QCD\] and \[\angle QBD\] also lie on the same segment QCBDQ of the circle.
So, \[\angle QCD = \angle QBD\] (2)
Now as we can see from the given figure that the line ABD and PBQ intersect each other at point B.
So, from the property of vertically opposite angles are equal we can say that,
\[ \Rightarrow \angle ABP = \angle QBD\] (3)
So, now using equation 1, 2 and 3 we can say that,
\[ \Rightarrow \angle ACP = \angle QCD\]
Hence Proved

Note:Whenever we face such types of questions then first, we have to prove that angles ABP and ACP are equal using the same segment property and then we can prove that angles QCD and QBD are also equal from the same segment property. And after that we had to show that ABP and QBD are equal from vertically opposite angles property. Then finally using these three equations we can show that angle ACP is equal to angle QCD. This will be the easiest and efficient way to find the solution of the problem.