
Two charges $2q$ and $ - 3q$ are fixed at points (4, 0, 0) and (9, 0, 0) respectively. The electric potential due to these charges will be zero on:
A) a spherical surface ${x^2} + {y^2} + {z^2} = 36$
B) a parábola ${y^2} = 36z$
C) an ellipsoidal $\dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{{81}} - {z^2} = 1$
D) a spherical surface ${\left( {x - 4} \right)^2} + {y^2} + {z^2} = 81$

Answer
588.3k+ views
Hint: Here, the electric potential due to the two charges must be zero at a point (x, y, z) which is at a distance $r$ from the origin. We need to find the equation of the surface on which (x, y, z) lies.
Formula used:
-The electric potential at a point P for a system of charges is given by, $V = k\left( {\dfrac{{{q_1}}}{{{r_{1P}}}} + \dfrac{{{q_2}}}{{{r_{2P}}}} + ............. + \dfrac{{{q_n}}}{{{r_{nP}}}}} \right)$ where ${q_1},{q_2},.........{q_n}$ are the charges placed at the distances ${r_{1P}},{r_{2P}},..........{r_{nP}}$ from the point P in space.
-The distance $s$ from a point at (a, b, c) is given by, $s = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} $
Complete step by step answer.
Step 1: List the data given in the question and sketch an appropriate figure.
The system under consideration consists of two charges $2q$ and $ - 3q$ placed at points (4, 0, 0) and (9, 0, 0) respectively.
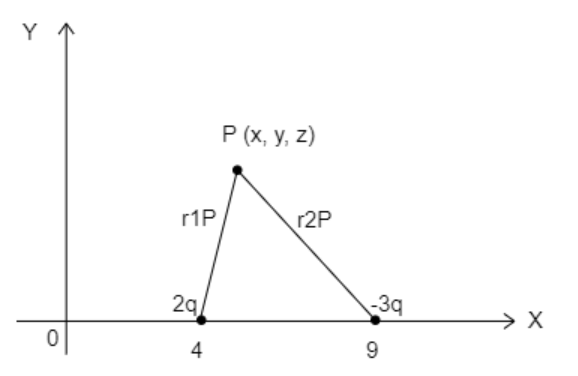
We consider the electric potential to be zero at some point P (x, y, z).
Let the charge $2q$ be at a distance ${r_{1P}}$ from the point P and let $ - 3q$ be at a distance ${r_{2P}}$ from the point P.
Step 2: Express the electric potential of the system.
The electric potential at a point P for a system of charges is given by, $V = k\left( {\dfrac{{{q_1}}}{{{r_{1P}}}} + \dfrac{{{q_2}}}{{{r_{2P}}}} + ............. + \dfrac{{{q_n}}}{{{r_{nP}}}}} \right)$ where ${q_1},{q_2},.........{q_n}$ are the charges placed at the distances ${r_{1P}},{r_{2P}},..........{r_{nP}}$ from the point P in space.
Here the system includes two charges ${q_1} = 2q$ and ${q_2} = - 3q$ which are at distances ${r_{1P}}$ and ${r_{2P}}$ from point P.
Then the electric potential at point P will be, $V = k\left( {\dfrac{{2q}}{{{r_{1P}}}} + \dfrac{{ - 3q}}{{{r_{2P}}}}} \right) = 0$ ------- (1)
Step 3: Solve equation (1) to get the equation of the surface on which the point P lies.
We have $k\left( {\dfrac{{2q}}{{{r_{1P}}}} + \dfrac{{ - 3q}}{{{r_{2P}}}}} \right) = 0$ or, $k\dfrac{{2q}}{{{r_{1P}}}} = k\dfrac{{3q}}{{{r_{2P}}}}$
Cancel out the similar terms on either side to get, $\dfrac{2}{{{r_{1P}}}} = \dfrac{3}{{{r_{2P}}}}$
Cross-multiplying the above relation we get, $2{r_{2P}} = 3{r_{1P}}$ -------(2)
The distance ${r_{1P}}$ can be expressed as ${r_{1P}} = \sqrt {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} $ --------- (3) since the charge $2q$ is placed at (4, 0, 0) from the origin.
Similarly, ${r_{2P}}$ can be expressed as ${r_{2P}} = \sqrt {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} $ ------------ (4) since the charge $ - 3q$ is placed at (9, 0, 0) from the origin.
Substituting equations (3) an (4) in equation (2) we get, $2\sqrt {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} = 3\sqrt {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} $
Squaring on both sides we get, $4\left[ {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} \right] = 9\left[ {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} \right]$
On expanding, we get $4{x^2} - 72x + 324 + 4{y^2} + 4{z^2} = 9{x^2} - 72x + 144 + 9{y^2} + 9{z^2}$
Simplifying we get, $5{x^2} + 5{y^2} + 5{z^2} = 180$ or ${x^2} + {y^2} + {z^2} = 36$ --------- (5)
Equation (5) represents a sphere of radius 6.
Therefore, the electric potential is zero on a spherical surface given by, ${x^2} + {y^2} + {z^2} = 36$ .
Hence the correct option is A.
Note: The point P lies on the spherical surface. The centre of the spherical surface is the origin. The terms ${\left( {x - 4} \right)^2}$ and ${\left( {x - 9} \right)^2}$ are expanded using the algebraic identity, ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$ .
Formula used:
-The electric potential at a point P for a system of charges is given by, $V = k\left( {\dfrac{{{q_1}}}{{{r_{1P}}}} + \dfrac{{{q_2}}}{{{r_{2P}}}} + ............. + \dfrac{{{q_n}}}{{{r_{nP}}}}} \right)$ where ${q_1},{q_2},.........{q_n}$ are the charges placed at the distances ${r_{1P}},{r_{2P}},..........{r_{nP}}$ from the point P in space.
-The distance $s$ from a point at (a, b, c) is given by, $s = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} $
Complete step by step answer.
Step 1: List the data given in the question and sketch an appropriate figure.
The system under consideration consists of two charges $2q$ and $ - 3q$ placed at points (4, 0, 0) and (9, 0, 0) respectively.
We consider the electric potential to be zero at some point P (x, y, z).
Let the charge $2q$ be at a distance ${r_{1P}}$ from the point P and let $ - 3q$ be at a distance ${r_{2P}}$ from the point P.

The figure represents point P in space
Step 2: Express the electric potential of the system.
The electric potential at a point P for a system of charges is given by, $V = k\left( {\dfrac{{{q_1}}}{{{r_{1P}}}} + \dfrac{{{q_2}}}{{{r_{2P}}}} + ............. + \dfrac{{{q_n}}}{{{r_{nP}}}}} \right)$ where ${q_1},{q_2},.........{q_n}$ are the charges placed at the distances ${r_{1P}},{r_{2P}},..........{r_{nP}}$ from the point P in space.
Here the system includes two charges ${q_1} = 2q$ and ${q_2} = - 3q$ which are at distances ${r_{1P}}$ and ${r_{2P}}$ from point P.
Then the electric potential at point P will be, $V = k\left( {\dfrac{{2q}}{{{r_{1P}}}} + \dfrac{{ - 3q}}{{{r_{2P}}}}} \right) = 0$ ------- (1)
Step 3: Solve equation (1) to get the equation of the surface on which the point P lies.
We have $k\left( {\dfrac{{2q}}{{{r_{1P}}}} + \dfrac{{ - 3q}}{{{r_{2P}}}}} \right) = 0$ or, $k\dfrac{{2q}}{{{r_{1P}}}} = k\dfrac{{3q}}{{{r_{2P}}}}$
Cancel out the similar terms on either side to get, $\dfrac{2}{{{r_{1P}}}} = \dfrac{3}{{{r_{2P}}}}$
Cross-multiplying the above relation we get, $2{r_{2P}} = 3{r_{1P}}$ -------(2)
The distance ${r_{1P}}$ can be expressed as ${r_{1P}} = \sqrt {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} $ --------- (3) since the charge $2q$ is placed at (4, 0, 0) from the origin.
Similarly, ${r_{2P}}$ can be expressed as ${r_{2P}} = \sqrt {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} $ ------------ (4) since the charge $ - 3q$ is placed at (9, 0, 0) from the origin.
Substituting equations (3) an (4) in equation (2) we get, $2\sqrt {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} = 3\sqrt {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} $
Squaring on both sides we get, $4\left[ {{{\left( {x - 9} \right)}^2} + {y^2} + {z^2}} \right] = 9\left[ {{{\left( {x - 4} \right)}^2} + {y^2} + {z^2}} \right]$
On expanding, we get $4{x^2} - 72x + 324 + 4{y^2} + 4{z^2} = 9{x^2} - 72x + 144 + 9{y^2} + 9{z^2}$
Simplifying we get, $5{x^2} + 5{y^2} + 5{z^2} = 180$ or ${x^2} + {y^2} + {z^2} = 36$ --------- (5)
Equation (5) represents a sphere of radius 6.
Therefore, the electric potential is zero on a spherical surface given by, ${x^2} + {y^2} + {z^2} = 36$ .
Hence the correct option is A.
Note: The point P lies on the spherical surface. The centre of the spherical surface is the origin. The terms ${\left( {x - 4} \right)^2}$ and ${\left( {x - 9} \right)^2}$ are expanded using the algebraic identity, ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$ .
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

Which are the Top 10 Largest Countries of the World?

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Giving reasons state the signs positive or negative class 12 physics CBSE

Explain esterification reaction with the help of a class 12 chemistry CBSE

What is defined as a solenoid Depict a diagram with class 12 physics CBSE




