Question

Two buildings are in front of each other on a road of width 10 meter. From the top of the first building which is 30 meter high, the angle of elevation to the top of the second is $45^\circ $. What is the height of the second building in meters?

Answer 1

Hint:
Here, we will draw a figure representing the given situation. We will use the trigonometric ratio in a triangle to find the difference between the heights of two buildings. We will add this difference to the remaining height which is equal to the height of other buildings to get the total height of the building.

Complete Step by step Solution:
Let the first building be $AB$.
And, let the second building be $CD$.
Now, the width between the two buildings $ = BD = 10{\text{m}}$
Also, it is given that the height of the first building, $AB = 30{\text{m}}$ and $\angle CAE = 45^\circ $ is the angle of elevation.
Hence, we will draw the following figure with the help of the given information, drawing a line $\text{ are} \parallel BD$ such that $AEDB$ is a rectangle with: $AE = BD = 10{\text{m}}$ and $AB = ED = 30{\text{m}}$

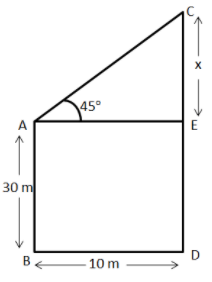
Now, let the length $CE = x$
From the figure, in the right angled triangle $\angle AEC$,
$\tan 45^\circ = \dfrac{P}{B} = \dfrac{{CE}}{{BD}}$
Substituting \[CE = x\] and $AE = BD = 10$ in the above equation, we get
$ \Rightarrow \tan 45^\circ = \dfrac{x}{{10}}$
We know that, $\tan 45^\circ = 1$, and substituting this value in the above equation, we get
$ \Rightarrow 1 = \dfrac{x}{{10}}$
Multiplying both sides by 10, we get
$ \Rightarrow x = 10{\text{m}}$
Now, from the figure,
The height of the second building $ = DE + CE$
Substituting $DE = 30$ and $CE = 10$ in the above equation, we get
$ \Rightarrow $ The height of the second building $ = 30 + 10 = 40{\text{m}}$

Therefore, the required height of the second building is 40 meters.

Note:
In the applications of trigonometry, the other type of question includes showing the angle of depression; we draw an imaginary line of sight which is always parallel to the base. The angle between that imaginary line of sight and the line joining the object is called the angle of depression. The angle of depression is always below the line of sight as it actually means ‘looking down’. Whereas, angle of elevation is always above the baseline as in simple terms it means ‘looking up’. The angle of elevation and the angle of depression are actually congruent to each other.