Question

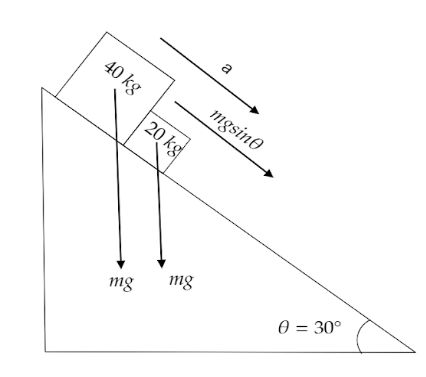
Two boxes, one of mass $20{\text{ }}kg$ and the other of mass $40{\text{ }}kg$, are sliding down a frictionless inclined plane that makes an angle of ${30^ \circ }$ with the horizontal. Find their respective acceleration.

Answer 1

Hint:When a body slips down an inclined plane the acceleration does not depend upon the mass. It only depends upon the acceleration due to gravity and the angle of inclination of the horizontal slope respectively.

Formula used:
$F = ma$
where $F$is the force, $m$ is the mass of the body and $a$ is the acceleration of the body.
The force experienced by an inclined body is $mg\sin \theta $. Now putting the value of $mg\sin \theta $ in $F = ma$ we get.
$mg\sin \theta = ma$
$ \Rightarrow a = g\sin \theta $
In this way, mass is not dependent upon any body inclining through a horizontal slope of any inclination angle.

Complete step by step answer:

It could be very easily solved from a formula that is being narrated below,
$a = g\sin \theta - - - - \left( 1 \right)$ where,
$g = $ acceleration due to gravity$ = 9.8{\text{ }}\dfrac{m}{{{s^2}}}$,
$\theta = $ the angle of inclination of the horizontal slope.
In the given question mass of the two bodies are given which are of no use here.
Given in the question,
$\theta = $${30^ \circ }$
Substituting the value of $\theta $ and $g$ in equation $\left( 1 \right)$ we get,
$a = 9.8 \times \sin {30^ \circ }$
And from trigonometric values we get $\sin {30^ \circ } = \dfrac{1}{2}$,
So, $a = 9.8 \times \dfrac{1}{2}$
$a = 4.9{\text{ }}\dfrac{m}{{{s^2}}}$
Thus, the acceleration of both the blocks are $4.9{\text{ }}\dfrac{m}{{{s^2}}}$ as both of their inclination angles are the same.

Note: There is not any dependence of mass in acceleration of any body inclining through any angle in a slope. It is dependent upon the angle of inclination. The mass is given only to distract the user. Acceleration due to gravity may change at places if the body is placed somewhere inside the earth or may be in space. We must not always rely on the constant value.