
Two bodies A and B of mass
Answer
509.1k+ views
Hint: For part (a) Calculate the amount of applied force that is spent to overcome friction by both bodies, and the resultant force will be equivalent to the reaction of the vertical wall, (b) Similar to part (a) except you calculate the amount of force spent on friction by A and B separately and remember that every action produces an equal and opposite reaction, and (c) If the bodies are in motion, remember that force due to acceleration becomes a contributing factor in addition to frictional and applied forces. Account for this force due to acceleration as well while calculating your net force.
Formula used:
Force
Frictional force
Complete answer:
Let us deconstruct the question to gain an understanding.
From the figure, we see that we have two bodies in contact with each and a force of
a.)Now, from Newton’s third law of motion we have that for every action, there is an equal and opposite reaction. Therefore, the net force that reaches the vertical wall will also be the normal reaction produced by the vertical wall, given by
b.)Now, let us analyse the action-reaction forces between A and B.
To transmit the applied force of
This gets spent from the applied force and the force applied by body A on body B will be
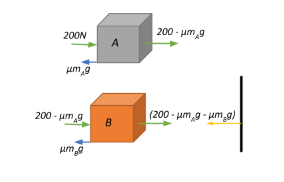
Now body B transmits this force to the wall but it has to overcome a friction of
If the wall is removed, the two bodies will move in the direction of the applied force and the net force acting on the moving system will be
c.)We now have to deduce if the force exerted by A on B will change if the bodies are in motion.
The equation of motion for this system of two bodies in acceleration can be written as:
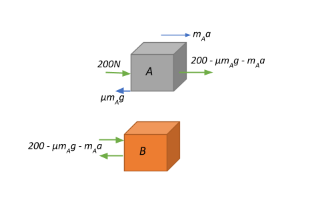
Thus, the force that contributes to the motion of A can be calculated:
This force gets spent from the force transmitted from A to B.
Therefore, the net force exerted by A on B will now be:
Note:
Remember to account for attenuation of the applied force due to friction and also due to acceleration. Overlooking these parameters will produce inconsistent results.
Also, notice that there is always a reaction produced from every component of the system when a force is applied. The best way to remember this is to just apply newton’s third law of motion in its most bare form.
And do not forget that friction and normal reaction are always in a direction opposite to the applied force, so calculate the net force at each point accordingly.
Formula used:
Force
Frictional force
Complete answer:
Let us deconstruct the question to gain an understanding.
From the figure, we see that we have two bodies in contact with each and a force of
a.)Now, from Newton’s third law of motion we have that for every action, there is an equal and opposite reaction. Therefore, the net force that reaches the vertical wall will also be the normal reaction produced by the vertical wall, given by
b.)Now, let us analyse the action-reaction forces between A and B.
To transmit the applied force of
This gets spent from the applied force and the force applied by body A on body B will be

Now body B transmits this force to the wall but it has to overcome a friction of
If the wall is removed, the two bodies will move in the direction of the applied force and the net force acting on the moving system will be
c.)We now have to deduce if the force exerted by A on B will change if the bodies are in motion.
The equation of motion for this system of two bodies in acceleration can be written as:

Thus, the force that contributes to the motion of A can be calculated:
This force gets spent from the force transmitted from A to B.
Therefore, the net force exerted by A on B will now be:
Note:
Remember to account for attenuation of the applied force due to friction and also due to acceleration. Overlooking these parameters will produce inconsistent results.
Also, notice that there is always a reaction produced from every component of the system when a force is applied. The best way to remember this is to just apply newton’s third law of motion in its most bare form.
And do not forget that friction and normal reaction are always in a direction opposite to the applied force, so calculate the net force at each point accordingly.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
The flightless birds Rhea Kiwi and Emu respectively class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE




