Question

Two blocks of masses 1kg and 3kg are connected by an inextensible string through a massless pulley as shown in the figure. All surfaces are smooth. A ball A of mass 1kg is moving towards a block of mass 1kg with a velocity 10m/s and collides in-elastically at t=0. Consider that there will be no jump of 3kg block at any time. Now match list 1 to list 2.

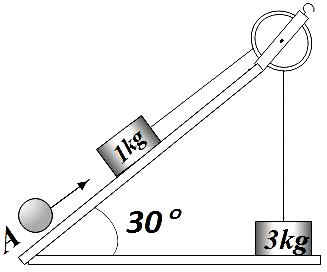
List 1	List 2
(P) The combined mass travels up the incline by a distance (in SI unit)	(1) 1
(Q) When combined mass comes back to its initial position, string regains its tension, then at the same moment velocity (In SI unit) of block of mass 3kg.	(2) 0.5
(R) The mass M moves up to a height (in SI unit) before stopping.	(3) 2
(S) Time (in SI unit) taken by 3kg block to rise up and come back to its initial position.	(4) 2.5

Answer 1

Hint: Find the velocity of the combined mass after collision using law of conservation of momentum and hence the required distance covered. Using the expression for impulse, find the required velocity. Draw the free body diagram of each body after the action of impulse and then balance the forces to get the acceleration. Now by using Newton’s equations of motion find the required quantities.
Formula used:
Impulse, $I=\Delta P=m\Delta v$
Newton’s equations of motion,
$v=u+at$
${{v}^{2}}-{{u}^{2}}=2as$

Complete answer:
When ball A of mass ${{m}_{b}}$moving with ${{v}_{b}}=10m{{s}^{-1}}$ collides with block of mass 1kg, the string become slack which further results in tension on the string becoming zero, also, since the collision is inelastic the ball gets attached to the block resulting in the net mass being 2kg. As all the force acting on the body at the moment is non impulsive, by conservation of momentum we have,
${{m}_{b}}{{v}_{b}}=\left( {{m}_{b}}+1 \right)u$
$\Rightarrow 1\times 10=2\times u$
$\Rightarrow u=\dfrac{10}{2}=5m{{s}^{-1}}$ ……………………….. (1)
So we get the velocity of the combined mass (ball +block of 1kg) after collision as $5m{{s}^{-1}}$.
Free body diagram of combined mass after collision,

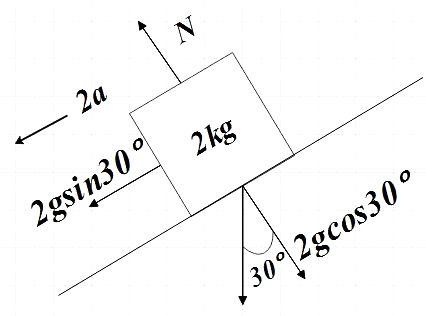
The net force on the body is given by,
${{F}_{net}}=ma=2g\sin 30$
$\Rightarrow 2a=2g\left( \dfrac{1}{2} \right)$
$\Rightarrow a=\dfrac{10}{2}=5m{{s}^{-2}}$ ……………………………….. (2)
After collision the combined mass will travel up the incline to reach a maximum height where its velocity is 0 covering a distance s.
From Newton’s equations,
${{v}^{2}}-{{u}^{2}}=2as$
From (1) and (2),
$0-25=2\times \left( -5 \right)\times s$
$\Rightarrow s=\dfrac{25}{10}=2.5m$
Therefore P is matched to (4).
When this combined mass reaches its initial position, the string regains its tension which will further provide impulse. This impulse will be the same on both the masses.
Impulse on combined mass,
$I=-2{{v}_{0}}-\left( -2\times 5 \right)=-2{{v}_{0}}+10$
Impulse on 3kg block,
$I=3{{v}_{0}}$
$\Rightarrow 3{{v}_{0}}=-2{{v}_{0}}+10$
$\Rightarrow {{v}_{0}}=\dfrac{10}{5}=2m{{s}^{-1}}$
Therefore Q is matched to (3).
After the action of impulse, the free body diagram becomes,

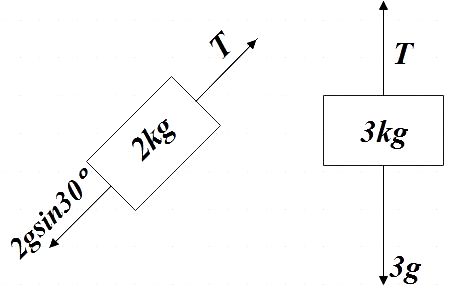
Net force on 2kg,
${{F}_{net}}=2a=T-2g\sin 30{}^\circ $
$T-g=2a$ ……………………………… (3)
Net force on 3kg,
${{F}_{net}}=3g-T=3a$ ………………………….. (4)
Adding (3) and (4),
$a=\dfrac{20}{5}=4m{{s}^{-2}}$ ……………………………. (5)
At maximum height h, v=0
${{v}^{2}}-{{u}^{2}}=2as$
$\Rightarrow 0-{{2}^{2}}=2\times \left( 4 \right)\times h$
$\Rightarrow h=\dfrac{1}{2}=0.5m$
Therefore, R is matched to (2)
Time taken for reaching the maximum height is given by,
$v=u+at$
$0=2-4t$
$t=\dfrac{1}{2}=0.5s$
Time taken by 3kg block to reach maximum height and back to its initial position will 2t,
$T=2t=0.5\times 2=1s$
Therefore, S is matched to (1).
Hence the answers are:
(P) The combined mass travels up the incline by a distance of 2.5m
(Q) When the combined mass comes back to its initial position, the string regains its tension, then at the same moment the velocity of the block of mass 3kg is $2m{{s}^{-1}}$.
(R) The mass M moves up to a height of 0.5m before stopping.
(S) Time taken by a 3kg block to rise up and come back to its initial position is 1s.

Note:
Most important factor that we should take care here is the sign convention. At each step accordingly use the sign convention for both acceleration as well as velocity. Also, try to imagine what actually happens for each body according to their mass and the force acting on them at a particular moment.