Question

Two billiard balls of the same size and mass are in contact on a billiard table. A third ball of the same size and mass strikes them symmetrically and remains at rest after the impact. The coefficient of restitution between the balls is:
(A) $ \dfrac{1}{2} $
(B) $ \dfrac{1}{3} $
(C) $ \dfrac{2}{3} $
(D) $ \dfrac{3}{4} $

Answer 1

Hint To solve this question, we need to apply the conservation of momentum, to find the final velocities of two of the balls in terms of the initial velocity of the third ball. Putting these in the expression of the coefficient of restitution, we will get the final answer.

Formula Used: The formula used in solving this question is given by
 $\Rightarrow e = \dfrac{{{v_S}}}{{{v_A}}} $ , here $ e $ is the coefficient of restitution, $ {v_S} $ is the velocity of separation, and $ {v_A} $ is the velocity of approach.

Complete step by step answer
Let the mass and the radius of each of the balls be $ m $ and $ r $ respectively. Let the initial velocity of the third ball be $ u $ , and the final velocities of the two balls be $ {v_1} $ , $ {v_2} $ at the angles $ {\theta _1} $ and $ {\theta _2} $ respectively with the horizontal. The collision is shown in the below figure.

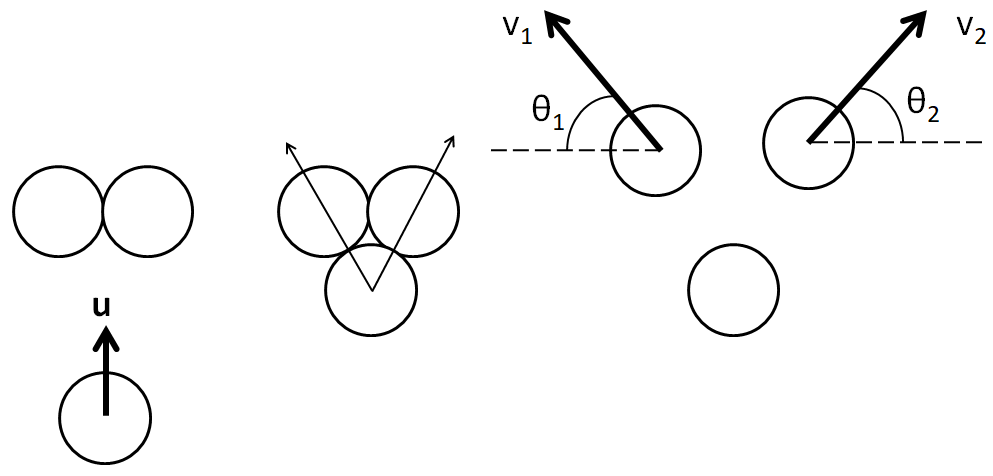
As there is no external force on the system of the three balls, so the total momentum is conserved. We first conserve the momentum in the vertical direction, and then in the horizontal direction.
Vertical direction:
Total initial momentum in the vertical direction
 $\Rightarrow {p_{iy}} = mu $ ……………………………….(1)
Total final momentum in the vertical direction
 $\Rightarrow {p_{fy}} = m{v_1}\sin {\theta _1} + m{v_2}\sin {\theta _2} $ ……………………..(2)
Equating (1) and (2) we have
 $ \Rightarrow mu = m{v_1}\sin {\theta _1} + m{v_2}\sin {\theta _2} $
Dividing by $ m $ , we get
 $\Rightarrow u = {v_1}\sin {\theta _1} + {v_2}\sin {\theta _2} $ ……………………….(3)
Horizontal direction:
Total initial momentum in the horizontal direction
 $\Rightarrow {p_{ix}} = 0 $ …………………………(4)
Total final momentum in the horizontal direction
 $\Rightarrow {p_{fx}} = m{v_2}\cos {\theta _2} - m{v_1}\cos {\theta _1} $ …………..(5)
Equating (4) and (5) we have
 $\Rightarrow 0 = m{v_2}\cos {\theta _2} - m{v_1}\cos {\theta _1} $
Dividing by $ m $ , we get
 $\Rightarrow 0 = {v_1}\cos {\theta _1} - {v_2}\cos {\theta _2} $
 $\Rightarrow {v_1}\cos {\theta _1} = {v_2}\cos {\theta _2} $
As the collision is symmetric, so we have $ {\theta _1} = {\theta _2} = \theta $
Substituting in the above equation we get
 $\Rightarrow {v_1}\cos \theta = {v_2}\cos \theta $
Dividing by $ \cos \theta $ , we get
 $\Rightarrow {v_1} = {v_2} = v{\text{ }}(say) $
So (3) becomes
 $\Rightarrow u = 2v\sin \theta $ ……………...(6)
Now, we know that the coefficient of restitution is given by
 $\Rightarrow e = \dfrac{{{v_S}}}{{{v_A}}} $ …………………...(7)
Considering the first two balls out of the three from the above figure.

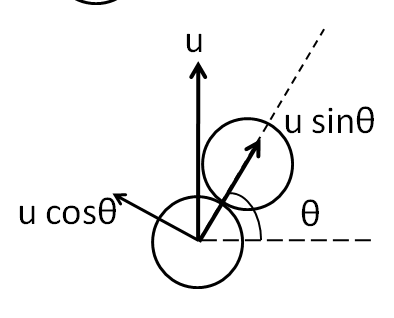
Taking the component of the velocity along the line of contact, we get the velocity of approach as
 $\Rightarrow {v_A} = u\sin \theta $ ………………….(8)
Now, after the collision, the third ball comes to rest, while the second ball moves with velocity $ v $ along the line of contact. Therefore, the velocity of separation is given by
 $\Rightarrow {v_S} = v $ ……………………………..(9)
Substituting (8) and (9) in (7) we get
 $\Rightarrow e = \dfrac{v}{{u\sin \theta }} $
Substituting (6)
 $\Rightarrow e = \dfrac{v}{{\left( {2v\sin \theta } \right)\sin \theta }} $
 $\Rightarrow e = \dfrac{1}{{2{{\sin }^2}\theta }} $ ……………….(10)
Now, we need the angle $ \theta $ . For this, we consider the geometry of the three balls as shown below.

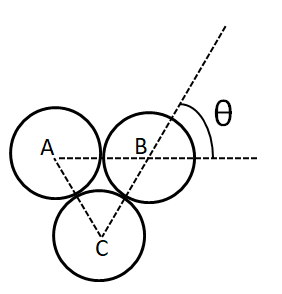
We have joined the centre A, B and C of the three balls and formed a triangle ABC. Since the radius of each ball is equal to $ r $ , so each side of the triangle is equal to $ 2r $ , i.e.
 $\Rightarrow AB = BC = CA = 2r $
So the triangle ABC is an equilateral triangle. We know that each angle of an equilateral triangle is equal to $ {60^ \circ } $ . So we have
 $\Rightarrow \angle ABC = {60^ \circ } $
Also, we have
 $\Rightarrow \theta = \angle ABC $ (Vertically opposite angles)
So, we get
 $\Rightarrow \theta = {60^ \circ } $
Putting this in (10) we have
 $\Rightarrow e = \dfrac{1}{{2{{\sin }^2}{{60}^ \circ }}} $
On solving we finally get
 $\Rightarrow e = \dfrac{2}{3} $
Thus the coefficient of restitution is equal to $ \dfrac{2}{3} $ .
Hence, the correct answer is option C.

Note
While calculating the coefficient of restitution, there is no need to consider the signs of velocity of approach or that of velocity of separation. Only their magnitudes are sufficient to be put in the expression.