Question

Two angles of a triangle are equal and the third angle is greater than each of those angles by $30^\circ $ . Determine all the angles of a triangle.

Answer 1

Hint: Assume the value of the equal angles to be $x$ . Then by the given condition we get the third angle to be $x + 30^\circ $ . By using the angle sum property, that is the sum of the angles of a triangle is $180^\circ $ , we get the value of $x$ . Using the value of $x$ , we can obtain the value of the angles of the triangle.

Complete answer:
Let the triangle be $\Delta ABC$ . Assume one of the angles of the triangle to be $\angle A = x$ .
We are given that the two angles are equal, so the second angle of the triangle is also $\angle B = x$ .
We are given that the third angle is greater than the other angles by $30^\circ $ .
Hence, we get the third angle to be $\angle C = x + 30^\circ $ .

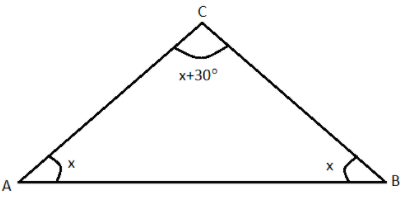
By the angle sum property of a triangle, we know that the sum of the three angles of a triangle is $180^\circ $ .
We get,
$x + x + x + 30^\circ = 180^\circ $
Adding the like terms, we get
$3x + 30^\circ = 180^\circ $
Subtracting $30^\circ $ on both sides we get
$3x + 30^\circ - 30^\circ = 180^\circ - 30^\circ $
$3x = 150^\circ $
Dividing by 3 on both sides we get the value of $x$
$\dfrac{{3x}}{3} = \dfrac{{150^\circ }}{3}$
$x = 50^\circ $
Now using this we get the value of the equal angles to be $50^\circ $
The third angle is obtained by substituting the value of $x$ in $x + 30^\circ $ .
The value of third angle is $50^\circ + 30^\circ = 80^\circ $
Therefore, the angles of the triangle are $50^\circ $ , $50^\circ $ and $80^\circ $ .

Note:
This is a problem. We have converted the given statement into a diagram; it helps us to visualise the problem and will enable us to think of an idea to solve the problem. Also, while drawing the diagram make sure that it meets all the given conditions. While solving for the value of the third angle we have to give more attention to simple addition and subtraction. There may be a chance of making mistakes in that part which may lead us to a wrong answer.