Question

Two adjacent sides of a parallelogram are in the ratio 5:7. If the perimeter of the parallelogram is 72 cm. Then find the value of sides of the parallelogram.

Answer 1

Hint: Assume the sides of a parallelogram to be multiple of x and hence assume the sides. Then use the formula “Perimeter of Parallelogram = 2 (One Side) + 2 (Other Side)” and substitute the given values to get the value of ‘x’. Then use this value of ‘x’ to get the values of adjacent sides.

Complete step-by-step answer:


To solve the given problem let’s assume a parallelogram ABCD given below,

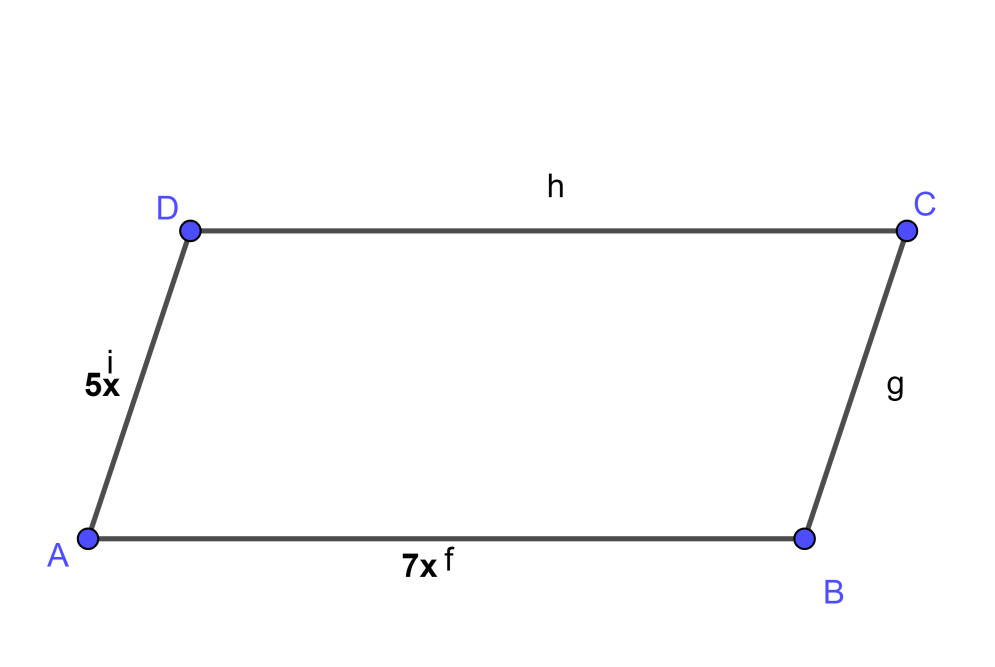
As we have given in the question that the ratio of two adjacent sides is 5:7

Therefore assume the two adjacent sides of the parallelogram as AD and AB and assume their value is in the multiple of ‘x’.

From above two statements we can write the value of sides of parallelogram as follows,

The smaller side AD = 5x cm ……………………………………………. (1)

The larger side AB = 7x cm ……………………………………………… (2)

Perimeter of Parallelogram ABCD = 72 cm ……………….. (3)

Now to proceed further in the solution we should know the formula given below,


Formula:

Perimeter of Parallelogram = 2 (One Side) + 2 (Other Side)

By using the above formula we can write the formula for perimeter of parallelogram ABCD as follows,

Perimeter of parallelogram ABCD = 2 (AD) + 2 (AB)

If we put the values of equation (1) and equation (2) in the above equation we will get,

Therefore, Perimeter of parallelogram ABCD = 2 (5x) + 2 (7x)

Therefore, Perimeter of parallelogram ABCD = 10x + 14x

If we put the value of equation (3) in the above equation we will get,

Therefore, 72 = 10x + 14x

Further simplification in the above equation will give,

Therefore, 24x = 72

If we shift 24 on the right hand side of the equation we will get,

$x=\dfrac{72}{24}$


Therefore, x = 3

If we put the value x = 3 in equation (1) we will get,

AD = $5\times 3$

Therefore, AD = 15 cm …………………………………………………………….. (4)

Also if we put x = 3 in equation (2) we will get,

AB = $7\times 3$

Therefore, AB = 21 cm ……………………………………………………………… (5)

From equation (5) and equation (6) we can write our final answer as,

The adjacent sides of a parallelogram having ratio as 5:7 and perimeter as 72 cm are 15 cm and 21 cm.

Note: There is no need to assume the parallelogram ABCD as you can directly solve the question by simply assuming the sides multiple of ‘x’ and then using the given conditions. Assuming a parallelogram will increase the length of your answer.