Question

How many triangles can be formed by joining the vertices of a hexagon?
A. 31
B. 25
C. 20
D. 60

Answer 1

Hint: As we know that hexagon has \[6\] vertices means \[6\] points and the triangle has \[3\] points means a triangle need \[3\] vertices to be formed. Then, the numbers of triangles that can be formed by joining the vertices of a hexagon can be calculated by applying the concept of combination.

Complete step by step solution:

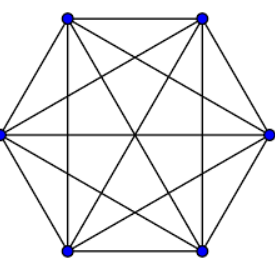
The number of vertices in a hexagon is \[6\].
The number of vertices in a triangle is \[3\].
That means to make a triangle we need \[3\] vertices.
So,\[6\]is the total number of vertices in hexagons, and out of those 6 vertices, 3 vertices that being chosen at a time to make a triangle.
By applying the formula of combination:
\[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\] where, n is the total numbers of objects and r is the number of objects to be chosen as a time.
Therefore,
\[{}^6{C_3} = \dfrac{{6!}}{{3! \times \left( {6 - 3} \right)!}} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}}\]
By using the values of factorial terms:
We have, \[6!\] can be written as \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\] can be written as \[3 \times 2 \times 1.\]
Replace \[6!\] = \[6 \times 5 \times 4 \times 3 \times 2 \times 1\] and \[3!\]= \[3 \times 2 \times 1\] in the following equation,
\[
  {}^6{C_3} = \dfrac{{6!}}{{3! \times \left( 3 \right)!}} \\
   = \dfrac{{6 \times 5 \times 4 \times 3 \times 2 \times 1}}{{3 \times 2 \times 1\left( {3 \times 2 \times 1} \right)}} = \dfrac{{120}}{6} = 20 \\
 \]
$\therefore$ The number of triangles that can be formed by joining the vertices of a hexagon is \[20\]. Hence, option (C) is correct.

Note:
These types of questions always use a combination concept for solving the problem.
Some important definitions you should know
Vertices mean the point where \[2\] or more lines meet.
Combination: Any of the ways we can combine things when the order does not matter.
Combination formula: The formula of combination is \[{}^n{C_r} = \dfrac{{n!}}{{r! \times \left( {n - r} \right)!}}\], where \[n\] represents the number of items and \[r\] represents the number of the items that being chosen at a time.
The factorial function\[(!)\]: The factorial function means to multiply all whole numbers from the chosen numbers down to \[1\].
The representation of factorial is \[n!\].
Alternatively, you can draw the figure and count the triangles but it becomes complicated.