Question

How many triangles can be drawn having angles \[53^\circ ,64^\circ ,63^\circ \] ?
A) \[1\]
B) \[2\]
C) $0$
D) More than \[2\]

Answer 1

Hint: In the above question, we are given three acute angles which are as \[53^\circ ,64^\circ ,63^\circ \] . We have to determine the number of triangles that can be formed having its three angles equal to the given three acute angles \[53^\circ ,64^\circ ,63^\circ \] . In order to approach the solution, we must keep in mind the angle sum property of a triangle which states that the sum of all three angles of a triangle is equal to \[180^\circ \] .

Complete step by step answer:
Given that, three angles are equal to \[53^\circ ,64^\circ ,63^\circ \] respectively.
We have to find the number of triangles that can be formed using the given three acute angles \[53^\circ ,64^\circ ,63^\circ \] .
Now, according to the angles sum property of a triangle, the sum to all three angles of a triangle is equal to \[180^\circ \] .
Hence, let us see if the given three acute angles hold the angle sum property or not.
We have the sum of given three acute angles \[53^\circ ,64^\circ ,63^\circ \] as,
\[ \Rightarrow 53^\circ + 64^\circ + 63^\circ = 180^\circ \]
Therefore, the three given acute angles \[53^\circ ,64^\circ ,63^\circ \] satisfy the angle sum property of a triangle.
Hence, they can form a triangle of any size, independent of the length of the three sides of the triangles as shown below.

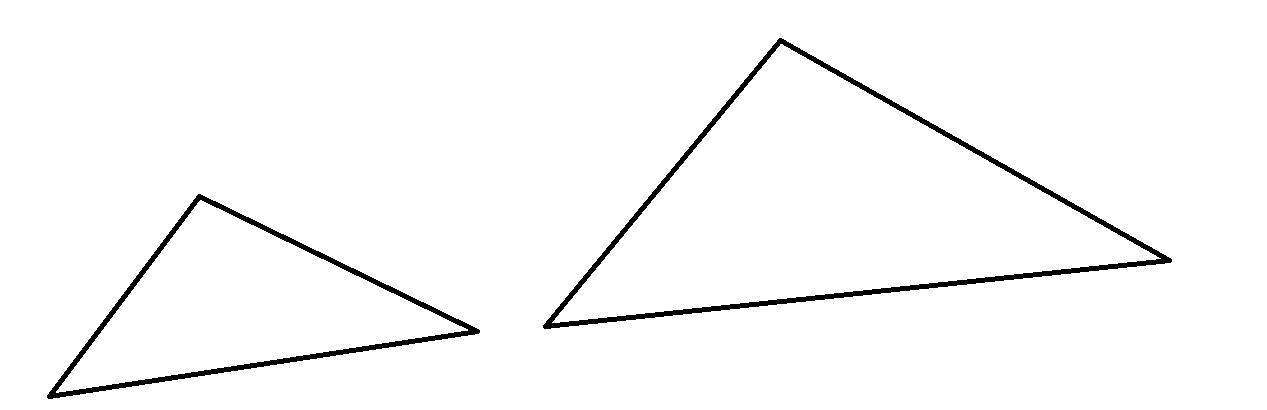
Since the length of the sides of the triangle is not given here.
That means, infinitely many triangles can be formed using the three angles \[53^\circ ,64^\circ ,63^\circ \] respectively.
That is definitely more than two triangles.
Therefore, the correct option is “D. More than \[2\] .”

Note:
There are different classifications of angles according to their values such as acute angles, right angles, obtuse angles, etc.
The angles which are less than \[90^\circ \] are called acute angles. Those having exactly a measure of \[90^\circ \] are called right angles. Angles greater than right angles but less than \[180^\circ \] are called obtuse angles. The angles having a measure of \[180^\circ \] are called straight angles. Whereas, the angles greater than straight angles but less than \[360^\circ \] are called reflex angles.