Question

Triangle $DEF$ in the figure is the right triangle with $\angle E = {90^ \circ }$ .
What type of angles are $\angle D$ and $\angle F$ ?

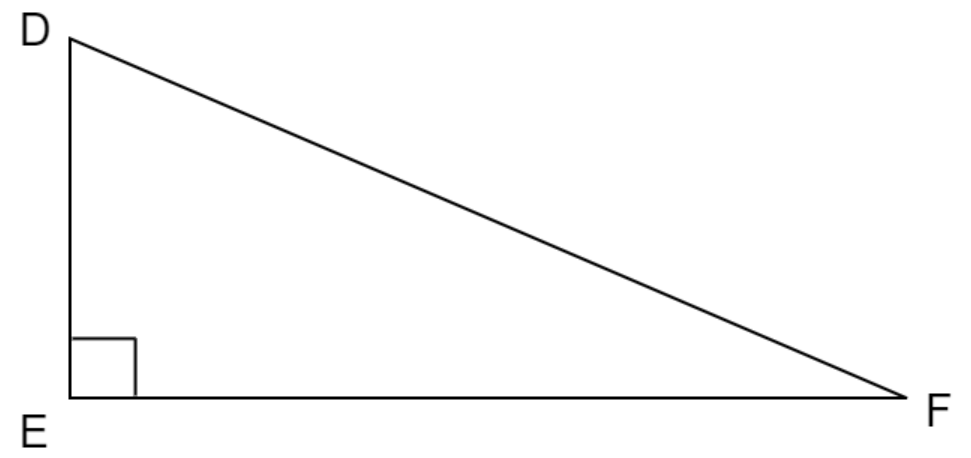
A). They are equal angles
B). They form a pair of adjacent angles
C). They are complementary angles
D). They are supplementary angles

Answer 1

Hint: We will use the angle sum property to the relationship between the angles of the triangle given in the figure. The angle sum property of a triangle states that the angles of a triangle always add up to ${180^ \circ }$. Every triangle has three angles and whether it is an acute, obtuse, or right triangle, the angles sum to ${180^ \circ }$.

Complete step-by-step solution:
The sum of interior angles of a triangle is ${180^ \circ }$ .
The angles of the triangle are $\angle D,\angle E{\text{ and }}\angle F$.
Now we will add the angles,
$\angle D + \angle E + \angle F = {180^ \circ }$
Substituting the value of $\angle E$ which is given in the question as ${90^ \circ }$ .
We get,
$\angle D + {90^ \circ } + \angle F = {180^ \circ }$
$\angle D + \angle F = {180^ \circ } - {90^ \circ }$
$\angle D + \angle F = {90^ \circ }$
From the above equation it is clear that the angles are complementary.
Therefore, the correct answer is option C. They are complementary angles.

Note: The sum of two interior angles of any triangle is always complementary. Two angles are said to be complementary if they add up to 90 degrees. Two complementary angles can be either adjacent or nonadjacent. Three or more angles cannot be complementary even if their sum is 90 degrees. When talking about complementary angles, always remember that the angles appear in pairs. One angle is the complement of the other angle.