Question

Triangle \[ABC\] is such that \[AB = 9cm, BC = 6cm, AC = 7.5\]. Triangle \[DEF\] is similar to \[\Delta ABC\]. If \[EF = 12cm\] then \[DE\] is:
${\text{(A) 6cm }}$
${\text{(B) 16cm }}$
${\text{(C) 18cm }}$
${\text{(D) 15cm }}$

Answer 1

Hint: To solve this geometry, use a similar triangle concept. Similar triangles, two figures having the same shape (but not necessarily the same size) are called similar figures.
Two triangles are said to be similar, if
Their corresponding angles are equal and
Their corresponding sides are in the same ratio proportion.
Using these conditions we can find the answer, especially when we use the second condition for this sum, because there is no angle in the problem, so we use the second condition to solve this sum.
Hence we get the answer.

Complete step-by-step answer:
Given that \[\Delta DEF\] is similar to \[\Delta ABC\]
 This is \[\;\Delta DEF \sim \Delta ABC\]
\[AB = 9cm,BC = 6cm,AC = 7.5\]
And \[EF = 12cm\]
The triangles will be
               

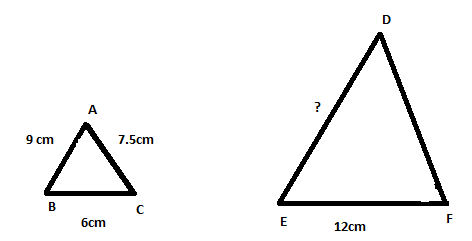
The condition two of similar triangle concept “Their corresponding sides are in the same ratio (or) proportion.”
Therefore,
\[\dfrac{{AB}}{{BC}} = \dfrac{{DE}}{{EF}}\]
Substitute the values of \[AB = 9cm,BC = 6cm,EF = 12cm\]
\[\dfrac{9}{6} = \dfrac{{DE}}{{12}}\]
Here, \[\dfrac{9}{6}\] can be written as \[\dfrac{{3 \times 3}}{{3 \times 2}}\]
Commonly cancel the \[3\] in the numerator and \[3\] in the denominator,
Therefore,
\[\dfrac{3}{2} = \dfrac{{DE}}{{12}}\]
Take that \[12\] to left hand side, and then it turns to multiply
\[\dfrac{3}{2} \times 12 = DE\]
\[12\] is \[6 \times 2\] and we can cancel the \[2\] in the numerator and cancel the \[2\] in the denominator.
\[DE = 3 \times 6\]
\[DE = 18\] cm

So, the correct answer is “Option C”.

Note: In a similar triangle, the corresponding sides are in the same ratio, the corresponding sides are proportional. That is, the ratios of the corresponding sides are equal.
Then the similar triangle corresponding angles are equal.
They are similar even if one is rotated, or one is a mirror image of the other.
The problem is not very difficult; also we can understand the concept of similar triangles.