Question

Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, we have \[\dfrac{AB}{PQ}=\dfrac{AD}{PM}\]. If the above statement is true, then mention the answer as 1, else mention it as 0 if false.

Answer 1

Hint: To check if the given statement is true or not, use the fact that if two triangles are similar, then their angles are equal and the altitude of a triangle is perpendicular to its base. Use AA (Angle – Angle) Property to prove that \[\Delta ABD\sim \Delta PQM\] and thus, the ratio of length of sides of two triangles will be equal.

Complete step-by-step answer:
We have two similar triangles \[\Delta ABC\] and \[\Delta PQR\]. AD and PM are altitudes of the two triangles. We have to check if the relation \[\dfrac{AB}{PQ}=\dfrac{AD}{PM}\] holds or not.

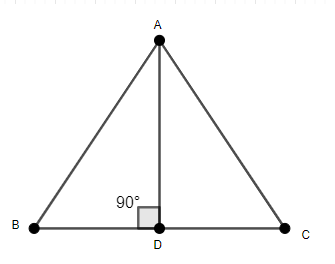
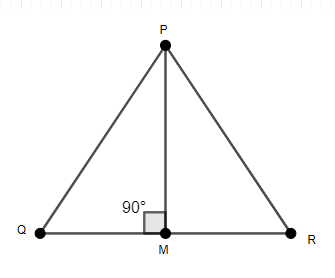
As \[\Delta ABC\sim \Delta PQR\], we know that the ratio of their corresponding sides is equal.
Thus, we have \[\dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{BC}{QR}\].
We will now consider the triangles \[\Delta ABD\] and \[\Delta PQM\].
We will prove that the two triangles are similar.
As AD is the altitude of \[\Delta ABC\], we have \[AD\bot BD\]. So, we have \[\angle ADB={{90}^{\circ }}\].
Similarly, as PM is the altitude of \[\Delta PQR\], we have \[PM\bot QM\]. So, we have \[\angle PMQ={{90}^{\circ }}\].
Thus, \[\angle PMQ=\angle ADB={{90}^{\circ }}\].
As we know that \[\Delta ABC\sim \Delta PQR\]. Thus, the corresponding angles of both the triangles are equal.
So, we have \[\angle PQM=\angle ABD\].
Thus, in \[\Delta ABD\] and \[\Delta PQM\], we have \[\angle PMQ=\angle ADB={{90}^{\circ }}\] and \[\angle PQM=\angle ABD\].
Using AA (Angle – Angle) Property, we have \[\Delta ABD\sim \Delta PQM\].
As \[\Delta ABD\sim \Delta PQM\], the ratio of length of sides of both the triangles is equal.
Thus, we have \[\dfrac{AB}{PQ}=\dfrac{AD}{PM}=\dfrac{BD}{QM}\].
So, the given statement is true.
Hence, the correct answer is 1.

Note: We can also prove that \[\Delta ABD\sim \Delta PQM\] by using the ASA (Angle Side Angle) Property as well. AA Property says that two corresponding angles of the triangles must be equal. ASA Property says that two corresponding angles and the sides between them of the two triangles must be equal.