Question

Triangle ABC is an equilateral triangle of side $2\sqrt 3 $cm. P is any point in the interior of triangle ABC, if x, y z are the distances of P from the sides of the triangle, then x + y+ z=?
$
  (a){\text{ 3cm}} \\
  {\text{(b) }}\left( {2 + \sqrt 3 } \right){\text{cm}} \\
  {\text{(c) 4cm}} \\
  {\text{(d) 5cm}} \\
 $

Answer 1

Hint – Equilateral triangles are the ones whose all three sides are equal. Compute the overall area of triangle ABC. It should be clear that the perpendicular distance of point P from the sides are given as x, y, z. So use this concept to compute individual areas of triangle APC, triangle APB and triangle BPC. Total area of the triangle will be the sum of these discrete triangle areas.

Complete step-by-step solution -

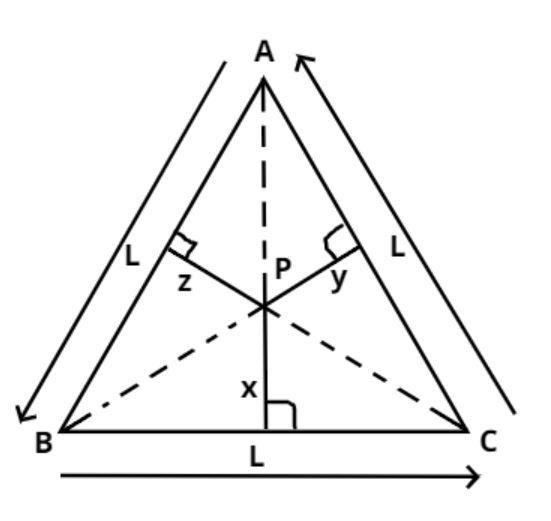
Consider the equilateral triangle ABC as shown above with side length L.
$ \Rightarrow L = 2\sqrt 3 $ cm (given).
Now as we know that the area (A) of the equilateral triangle is $\dfrac{{\sqrt 3 }}{4}{\left( {{\text{Side}}} \right)^2}$.
$ \Rightarrow A = \dfrac{{\sqrt 3 }}{4}{\left( L \right)^2}$ sq. cm.
Let P be any point inside the equilateral triangle as shown in figure and x, y and z are the distances from the point P on the sides BC, AC and AB as shown in figure.
Where x, y and z are the perpendicular distances from the point P on the sides BC, AC and AB as shown in figure.
Now as we know that the area of the triangle is half multiplied by base time’s height.
So in triangle APC
$ \Rightarrow {A_1} = \dfrac{1}{2}\left( {AC} \right)\left( y \right) = \dfrac{1}{2}\left( L \right)\left( y \right)$ sq.cm………………………. (1)
Similarly in triangles APB and BPC,
$ \Rightarrow {A_2} = \dfrac{1}{2}\left( {AB} \right)\left( y \right) = \dfrac{1}{2}\left( L \right)\left( z \right)$ sq.cm………………………. (2)
$ \Rightarrow {A_3} = \dfrac{1}{2}\left( {BC} \right)\left( x \right) = \dfrac{1}{2}\left( L \right)\left( x \right)$ sq.cm……………………….. (3)
Now add equation (1), (2) and (3) we have
$ \Rightarrow {A_1} + {A_2} + {A_3} = \dfrac{1}{2}\left( L \right)\left( y \right) + \dfrac{1}{2}\left( L \right)\left( z \right) + \dfrac{1}{2}\left( L \right)\left( x \right)$ sq.cm
Now the sum of all the triangle areas is equal to the area of the big triangle.
$ \Rightarrow A = {A_1} + {A_2} + {A_3}$
So substitute the values in the above equation we have,
$ \Rightarrow \dfrac{{\sqrt 3 }}{4}{\left( L \right)^2} = \dfrac{1}{2}\left( L \right)\left( y \right) + \dfrac{1}{2}\left( L \right)\left( z \right) + \dfrac{1}{2}\left( L \right)\left( x \right)$
Now simplify it we have,
$ \Rightarrow \dfrac{{\sqrt 3 }}{2}\left( L \right) = x + y + z$
Now substitute the value of L we have,
$ \Rightarrow x + y + z = \dfrac{{\sqrt 3 }}{2}\left( {2\sqrt 3 } \right) = \sqrt 3  \times \sqrt 3  = 3$.
So this the required value of (x + y + z).
Hence option (A) is correct.

Note – Whenever we face such types of problems the key concept is to have a good grasp of the basic formulas like area of equilateral triangle, area of basic triangle. This formula helps in evaluation of problems and helps in evaluation of the answer.