Question

Top view of a block on a table is shown $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{~s}^{2}\right)$
Find out the acceleration of the block.

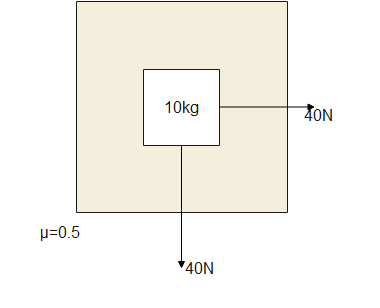
A.$0.6$
B.$0.8$
C.$1.6$
D.$0.5$

Answer 1

Hint: In mechanics, acceleration is the rate at which an object's velocity varies in relation to time. Accelerations are (in that they have magnitude and direction) vector quantities. The orientation of the acceleration of an object is provided by the orientation of the net force which acts on that object.
Formula used: $\mathrm{a}=\dfrac{\mathrm{F}_{\mathrm{R}}-\mathrm{I}_{\mathrm{s} \max }}{\mathrm{m}}$
(a)= acceleration of the body
(m)= mass of the body
(f)= force on the body

Complete answer:
The force of friction depends on an object's mass plus the sliding friction coefficient between the object and the surface on which it slides. To find the object's acceleration, deduct this force from the applied force. In Newton's second law, the formula is acceleration (a) equal to friction (F) divided by its Acceleration(a) \[\text{a=F+m}\]
Now $\mathrm{f}_{\mathrm{s}} \leq \mu \mathrm{N}$
$\therefore \mathrm{f}_{\mathrm{s}} \leq 50$
$\mathrm{F}_{\mathrm{R}}>\mathrm{f}_{\mathrm{smax}}$
Hence the block will move
$\Rightarrow \text{a}=\dfrac{{{\text{F}}_{\text{R}}}-{{\text{f}}_{\text{s}\max }}}{\text{m}}$
$\Rightarrow \text{a}=\dfrac{56-50}{10}$
$\therefore (\text{a)=}0.6~\text{m}/~{{\text{s}}^{2}}$
\[\therefore \] Block will move with a acceleration of $0.6~\text{m}/~{{\text{s}}^{2}}$

Option (A) should be selected

Additional Information:
Generally, Calculation of the acceleration of an object of mass (m) according to the force F applied and the force of friction. You use the coefficient of sliding friction to get this result as the object is moving:
\[a=\dfrac{{{F}_{app}}~-\text{ }{{\mu }_{sl}}~\times \text{ }mg}{m}\]
The second law of Newton states that an object's acceleration (a) is proportional to the force (F) applied to it, and the proportionality factor is the mass of the object (m).

Note:
Create an incline plane from one of the materials to identify the minimum coefficient of static friction between two materials and put a body made of the other material on it. Increase the tilt angle until the body begins to slip. The coefficient of friction is the tangent of the angle. This coefficient depends on the characteristics of the two surfaces that are in contact with each other.