Question

To solve the trigonometric equation which is given as $\dfrac{\cos 45}{\sec 30}+\cos ec30$.

Answer 1

Hint: To solve this problem, we need to be aware about the basic concepts of trigonometric angles and their value. Then, we can substitute the values to solve the following expression.

Complete step-by-step solution -
We first try to understand the trigonometric properties in terms of a right triangle ABC (as shown below). This would be helpful to express values of sec A and cosec A in terms of cos A and sin A.

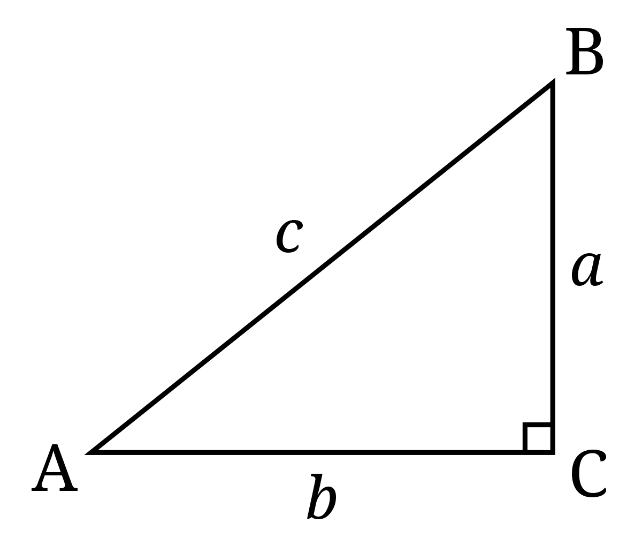
Now, by definition, we have,
sin A = $\dfrac{a}{c}$ -- (1)
cos A = $\dfrac{b}{c}$ -- (2)
By definition, we have,
sec A = $\dfrac{c}{b}$ -- (3)
cosec A = $\dfrac{c}{a}$ -- (4)
Now, we have to evaluate the expression $\dfrac{\cos 45}{\sec 30}+\cos ec30$. Thus, expressing the values of sec A and cosec A in terms of cos A and sin A by using the results of (3) and (4), we have,
= (cos 45)(cos 30) + $\dfrac{1}{\sin 30}$
= $\dfrac{1}{\sqrt{2}}\dfrac{\sqrt{3}}{2}+\dfrac{1}{\dfrac{1}{2}}$
= $\dfrac{1}{\sqrt{2}}\dfrac{\sqrt{3}}{2}+2$
= $\dfrac{\sqrt{3}}{2\sqrt{2}}+2$
Hence, the answer of $\dfrac{\cos 45}{\sec 30}+\cos ec30$, is $\dfrac{\sqrt{3}}{2\sqrt{2}}+2$.

Note: While evaluating trigonometric angles, it is always useful to bring the terms in the form of known quantities. Thus, it is always better to convert sec x, cosec x and cot x in terms of cos x, sin x and tan x. This is because most of the trigonometric identities and the formula values are known in the form of cos x, sin x and tan x. At times, it is also better to remember the trigonometric identities like $\sin (A+B)=\sin A\cos B+\cos A\sin B$, since some of the trigonometric expressions can be simplified using this rule, which makes the problem less tedious.