Question

How is the time period $ T $ and frequency $ f $ of a simple pendulum related to each other?

Answer 1

Hint: Simple pendulums have oscillatory and periodic motions. Time period is defined as the time taken by the bob of a pendulum to finish a left swing and a right swing of. Frequency is defined as the number of oscillations made by the bob of the pendulum per second. The frequency and time period of an oscillation are inversely related to each other.

Complete step by step answer:
The motions of the simple pendulum are oscillatory and periodic. The to and fro motion of a particle is said to be oscillatory and the motion that repeats itself after equal intervals is said to be periodic.
The simple pendulum consists of a point mass suspended from a massless flexible and inextensible string clamped to a right support. The ideal simple pendulum as defined above is not possible. In ideal practice, the simple pendulum consists of a heavy spherical bob suspended with a flexible and inextensible string from a rigid support.

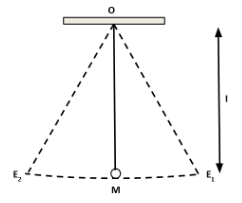
The distance between the point of suspension $ O $ and the center of gravity $ g $ of the bob is called the length of the simple pendulum. It is denoted by $ l $ . Then the time period of the pendulum is given by
$ T = 2\pi \sqrt {\dfrac{l}{g}} $
Time period is actually the time taken by the bob of a pendulum to finish one cycle that is a left swing and a right swing. Frequency is defined as the number oscillations made by the bob of the pendulum per second. Thus, frequency is written as the reciprocal of the time period of the pendulum.
Therefore, $ f = \dfrac{1}{T} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{g}{l}} $
Hence, the time period $ T $ and frequency $ f $ of a simple pendulum related to each other as $ f = \dfrac{1}{T} $.

Note:
Other factors that affect the time period of the pendulum are the length of the pendulum, the weight of the bob, the center of gravity and the amplitude of oscillations. The above mentioned equations of time period and frequency are valid only when the amplitude of the simple pendulum is small and the length is finite.