Question

How many tiles whose length and breadth are 12cm and 5cm respectively will be needed to cover a rectangular region whose length and breadth are respectively: 144cm and 1m.

Answer 1

Hint: The number of required tiles will be the area of the rectangular region by the area of the tile. Thus find the area of the rectangular region and tile separately. Then divide them to get the number of tiles that will fit in the rectangular region.

Complete step-by-step answer:
We have been given a rectangle of length and breadth are 100cm and 144cm.
Here, 1m = 100cm.
\[\therefore \] Length and breadth of rectangle = 100cm and 144cm.

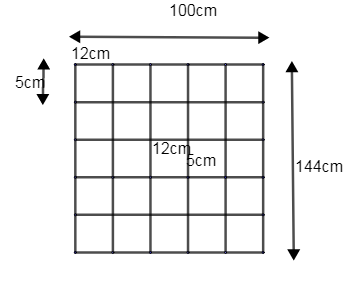
Now we have been given the length and breadth of a tile as 12cm and 5cm.
From the figure you can understand that we need to find the number of tiles that will fit in the rectangle. Thus to get the number of tiles, we have to decide the area of tiles from the area of the rectangle.
\[\therefore \] $\text{Number of tiles} = \dfrac{\text{Area of rectangular region}}{\text{Area of rectangular tile}}$.
Now, let us first find the area of the rectangular tile.

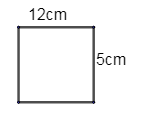
We know, the length = 12cm and breadth = 5cm.
\[\therefore \] Area of a rectangle = length \[\times \] breadth
\[\therefore \] Area of rectangular tile = 12 \[\times \] 5 = 60 \[c{{m}^{2}}\].
Hence, we got the area of the rectangular tile as 60 \[c{{m}^{2}}\].
Now let us find the area of the rectangular region.

Length of the region = 100cm.
Breadth of the region = 144cm.
\[\therefore \] Area of a region = length \[\times \] breadth
\[\therefore \] Area of rectangle = 100 \[\times \] 144 = 14400 \[c{{m}^{2}}\].
Thus, we got the area of the rectangle = 14400 \[c{{m}^{2}}\].
\[\therefore \] Number of tiles = Area of rectangular region / Area of rectangular tile = \[\dfrac{14400}{60}=240\]
\[\therefore \] 240 tiles are required to cover the region.
 Hence we got the number of tiles as 240.

Note: Draw a figure, so that you might understand the question better. These are some basic applications of rectangles. We can similarly find the number of square files that can fit in a square etc.