Question

Through the vertex O of the parabola ${{y}^{2}}=4ax$ two chords OP & OQ are drawn and the circles on OP & OP as diameters intersect in R. If ${{\theta }_{1}},{{\theta }_{2}}\And \phi $ are the angles made with the axis by the tangents at P & Q on the parabola & by OR then the value of, $\cot {{\theta }_{1}}+\cot {{\theta }_{2}}=$
A. $-2\tan \phi $
B. $-2\tan \left( \pi -\phi \right)$
C. 0
D. $2\cot \phi $

Answer 1

Hint: Use application of derivative to find slope of tangents through P and Q. Equation of common chord of two circles ${{S}_{1}}$ and ${{S}_{2}}$ can be given by relation ${{S}_{1}}-{{S}_{2}}=0$. Eliminate extra variables to get a solution.

Complete step-by-step answer:

Here, we have an equation of the parabola with vertex at 0.

Now, we have two chords OP and OQ in figure 1 and drawn two circles on OP and OQ as diameters such that circles intersect at R. Hence diagram can be drawn as:-

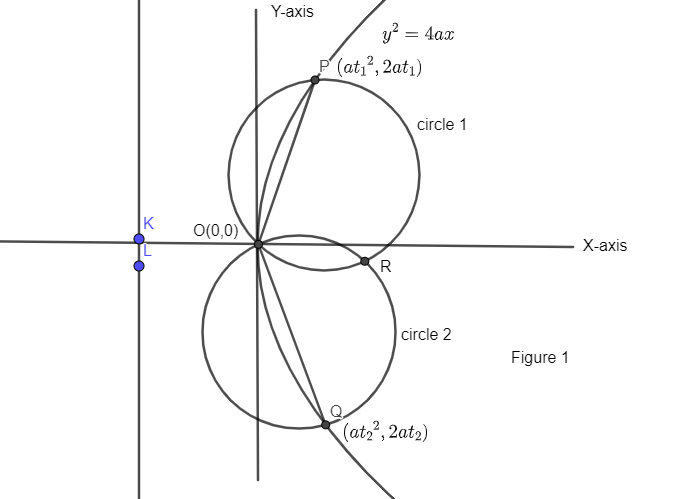
Now, let us assume two parametric coordinates at given parabola ${{y}^{2}}=4ax$.

As we know parametric coordinates for ${{y}^{2}}=4ax$ is given as $\left( a{{t}^{2}},2at \right)$.

Hence, suppose point P and Q have parametric coordinates at $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ respectively.

So, we have coordinates of diameters of both circles as shown in figure 1.

We know that equation of circle can be given as

$\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$ If $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the endpoints and diameter of the circle.

Hence, equation of circle with diameter ‘OP’ i.e. circle 1 is given as

$\left( x-0 \right)\left( x-a{{t}_{1}}^{2} \right)+\left( y-0 \right)\left( y-2a{{t}_{1}} \right)=0$

$x\left( x-a{{t}_{1}}^{2} \right)+y\left( y-2a{{t}_{1}} \right)=0$

Simplifying the above relation, we get

${{x}^{2}}+{{y}^{2}}-a{{t}_{1}}^{2}x-2a{{t}_{1}}y=0\ldots \ldots (2)$

Similarly, equation of circle with OQ as a diameter is given as

$\begin{align}

  & \left( x-0 \right)\left( x-a{{t}_{2}}^{2} \right)+\left( y-0 \right)\left( y-2a{{t}_{2}} \right)=0 \\

 & \Rightarrow x\left( x-a{{t}_{2}}^{2} \right)+y\left( y-2a{{t}_{2}} \right)=0 \\

\end{align}$

On simplifying, we get

${{x}^{2}}+{{y}^{2}}-a{{t}_{2}}^{2}x-2a{{t}_{2}}y=0\ldots \ldots (3)$

Now, coming to the question again, we have been provided angles with the X-axis of tangent through P and Q on parabola and angle with the X-axis of OR is also given.

We know slope is defined as the ‘tan’ angle of any line with the X-axis.

Angles of tangent through P and Q are given as ${{\theta }_{1}}$ and ${{\theta }_{2}}$.

Hence slope of tangent through P be $\tan {{\theta }_{1}}$ and slope of tangent through Q be $\tan {{\theta }_{2}}$.

And the slope of the line OR be $\tan \phi $ as $\phi $ is the angle OR forming an X-axis.

Now, we know that the slope of a tangent through any curve $f\left( x,y \right)$ can be calculated by finding the derivative of that curve at that particular point.

Hence, slope of tangent through ‘P’ is given as $\phi $.

We have the equation of parabola as ${{y}^{2}}=4ax$.

Differentiating it w.r.t x on both sides, we get

$2y\dfrac{dy}{dx}=4a$ as $\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$

$\dfrac{dy}{dx}=\dfrac{4a}{2y}=\left( \dfrac{2a}{y} \right)\ldots \ldots (4)$.

Slope of tangent at $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ can be given as,

${{\dfrac{dy}{dx}}_{\left| \left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)
\right.}}=\dfrac{2a}{2a{{t}_{1}}}=\dfrac{1}{{{t}_{1}}}\ldots \ldots (5)$

Similarly, slope of tangent through Q can be given by equation (4) as

${{\dfrac{dy}{dx}}_{\left| \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)
\right.}}=\dfrac{2a}{2a{{t}_{2}}}=\dfrac{1}{{{t}_{2}}}\ldots \ldots (6)$

As we already know that slope of tangent through P and Q is given in the problem as $\tan {{\theta }_{1}}$ and $\tan {{\theta }_{2}}$.

Hence, from equation (5) and equation (6), we get

$\tan {{\theta }_{1}}=\dfrac{1}{{{t}_{1}}}\And \tan {{\theta }_{2}}=\dfrac{1}{{{t}_{2}}}\ldots \ldots (7)$

Now, for calculating slope of OR, we need to calculate equation of OR as:-

If we have two circles ${{S}_{1}}$ and ${{S}_{2}}$ then equation of their common chord is given as ${{S}_{1}}-{{S}_{2}}=0$.

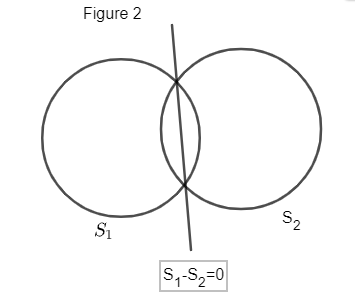
As OR is a common chord of both circles in figure 1.

Hence equation of common chord can be calculated from equation (2) and (3) as

$\left( {{x}^{2}}+{{y}^{2}}-a{{t}_{1}}^{2}x-2a{{t}_{1}}y \right)-\left(
{{x}^{2}}+{{y}^{2}}-a{{t}_{2}}^{2}x-2a{{t}_{2}}y \right)=0$

On simplifying above, we get

$\begin{align}

  & -a{{t}_{1}}^{2}x-2a{{t}_{1}}y+a{{t}_{2}}^{2}x+2a{{t}_{2}}y=0 \\

 & \Rightarrow a{{t}_{2}}^{2}x-a{{t}_{1}}^{2}x+2a{{t}_{2}}y-2a{{t}_{1}}y=0 \\

 & \Rightarrow ax\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)+2ya\left( {{t}_{2}}-{{t}_{1}} \right)=0
\\

\end{align}$

We know algebraic identity

\[{{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\], so above equation can be written as

\[ax\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)+2ya\left( {{t}_{2}}-{{t}_{1}}
\right)=0\]

Taking \[\left( {{t}_{2}}-{{t}_{1}} \right)\] common, we get

\[\left( {{t}_{2}}-{{t}_{1}} \right)\left[ ax\left( {{t}_{2}}+{{t}_{1}} \right)+2ya \right]=0\]

As \[{{t}_{1}}\ne {{t}_{2}}\], hence

\[\begin{align}

  & 2ay=-ax({{t}_{1}}+{{t}_{2}}) \\

 & \Rightarrow y=-\left( \dfrac{{{t}_{1}}+{{t}_{2}}}{2} \right)x\ldots \ldots (8) \\

\end{align}\]

Now, comparing equation (8) by \[y=mx+c\], we get slope ‘m’ be \[-\left( \dfrac{{{t}_{1}}+{{t}_{2}}}{2} \right)\] and ‘c’ be 0.

Hence, slope of the line is \[-\left( \dfrac{{{t}_{1}}+{{t}_{2}}}{2} \right)\].

Now, we already know the slope of the line OR be $\tan \phi $ as given in the problem.
Therefore, we get

\[\tan \phi =-\left( \dfrac{{{t}_{1}}+{{t}_{2}}}{2} \right)\ldots \ldots (9)\]

Now, from equation (7) we have,

$\tan {{\theta }_{1}}=\dfrac{1}{{{t}_{1}}}\And \tan {{\theta }_{2}}=\dfrac{1}{{{t}_{2}}}$

 ${{t}_{1}}=\dfrac{1}{\tan {{\theta }_{1}}}\And {{t}_{2}}=\dfrac{1}{\tan {{\theta }_{2}}}$

We know \[\dfrac{1}{\tan x}=\cot x\], hence we get,

\[{{t}_{1}}=\cot {{\theta }_{1}}\And {{t}_{2}}=\cot {{\theta }_{2}}\ldots \ldots (10)\]

Putting values of \[{{t}_{1}}\] and \[{{t}_{2}}\] from equation (10) in equation (9), we get

\[\begin{align}

  & \tan \phi =-\dfrac{\left( \cot {{\theta }_{1}}+\cot {{\theta }_{2}} \right)}{2} \\

 & \Rightarrow \cot {{\theta }_{1}}+\cot {{\theta }_{2}}=-2\tan \phi \\

\end{align}\]

Therefore, the value of \[\cot {{\theta }_{1}}+\cot {{\theta }_{2}}\]is \[-2\tan \phi \].

Hence, option A is correct.

Note: One can find slopes of tangents by writing tangent equations at P and Q with respect to parabola ${{y}^{2}}=4ax$ as well. We know that tangent at \[\left( {{x}_{1}},{{y}_{1}} \right)\] on parabola ${{y}^{2}}=4ax$ is given as T=0 or \[y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)\]. Put \[\left( {{x}_{1}},{{y}_{1}} \right)\] values as coordinates of P and Q then relate that equation with \[y=mx+c\] to get slopes. Finding slopes of line OR is the key point of this question. One can go for calculating point ‘R’ as well by solving the equations of both circles. But, it will be a complex way and much longer than the given solution.
One can suppose points P and Q as \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] but need to use relationship \[{{y}_{1}}^{2}=4a{{x}_{1}}\] and \[{{y}_{2}}^{2}=4a{{x}_{2}}\] for eliminating \[{{x}_{1}},{{x}_{2}},{{y}_{1}}\] and \[{{y}_{2}}\]. It will be longer as well as the given solution as coordinates are taken in parametric form which makes the solution more flexible.
Hence, supposing parametric coordinates in conic sections always help to solve the questions easily.