Question

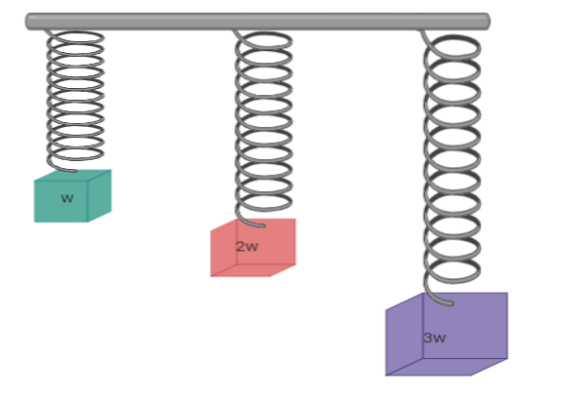
Three weights $w$, $2w$, \[3w\] are connected to identical springs suspended from a rigid horizontal rod. The assembly of the rod and weights falls freely. The positions of the weight from the rod are such that
A. $3w$ will be farthest
B. $w$ will be farthest
C. All will be at the same distance
D. $2w$ will be farthest

Answer 1

Hint:When a body freely falls, It’s apparent weight becomes zero. This is due to the Pseudo force. This effect was first explained by Newton.

Pseudo Force:- A Pseudo force is an apparent force that acts on all masses whose motion is described using a non-inertial frame of the reference frame.
Pseudo Force ${F_p}$ = m (mass of object) $\times$ a(acceleration of noninertial frame)

Non-Inertial Frame:-A non-inertial reference frame is a frame of reference that is undergoing acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration.

Complete step by step solution:
When the whole assembly is in rest, springs will be in the stretched position.
$Spring{\text{ }}Force{F_s} = kx$
Where , $k = $ Stiffness of springs
$x = $ Elongation in spring

As we can see,
$x \propto {F_s}$
In our case
${F_s} = $ Weight of body
So $x\left( {elongation} \right)$ will be more for $3w$.

Now when assembly falls freely with gravitational acceleration. A pseudo force will act on all bodies.

So, the
Pseudo Force ${F_p}$ = m(mass of body) $\times g$
(Note:- Assembly is falling with gravitational acceleration)
And
$m\left( {mass{\text{ }}of{\text{ }}body} \right) = \dfrac{{weight{\text{ }}of{\text{ }}body}}{g}$
So,
 ${F_p} = \left( {\dfrac{{weight{\text{ }}of{\text{ }}body}}{g} \times g} \right)$
Finally
${F_p} = $ Weight of body
From Free body diagram of the body
The resultant force on spring
${F_s} = \left( {Weight{\text{ }}of{\text{ }}body - {F_p}} \right)$
${F_s} = 0$
So there will be no force acting on spring. Spring will come in an unstretched position.
Now when all the springs are identical. So all springs will be at the same level and all the weights will be at equal distances from the rod.

So our option (C) is the right answer.

Note:The whole assembly is falling freely. So all weights are weightless during free fall. As there is no weight and also there will be no force on springs. Springs will be unstretched and all weights will be at the same level.