Question

Three waves due to three coherent sources meet at one point. Their amplitudes are $\sqrt 2 {A_0}$, $3{A_0}$ and, $\sqrt 2 {A_0}$intensity corresponding to ${A_0}$is ${I_0}$. Phase difference between first and second is $45^\circ $. Path difference between first and third $\dfrac{\lambda }{4}$. In phase angle, the first wave lags behind the other two waves. Find resultant intensity at this point.

Answer 1

Hint:
> The path difference between the 1st wave and the 3rd wave is given. We need to convert it into a phase difference. After getting the two phase differences it is easy to draw the diagram of waves’ directions.
> Using the diagram and given data the resultant amplitude can be calculated from the formula of resultant amplitude.
> Since there is a relationship between the intensity and amplitude we can easily get the value of the intensity from the amplitude.
Formula used:
Phase difference = $\dfrac{{2\pi }}{\lambda } \times $ Path difference.
The resultant amplitude of two waves ${A_1}$ and ${A_2}$is, ${A_R} = \sqrt {{A_1}^2 + {A_2}^2 + 2{A_1}{A_2}\cos \theta } $
The intensity $I \propto {A^2}$ , $A = $ amplitude.

Complete step-by-step solution:
Three waves from the three coherent sources meet at one point.
Given that, the Phase difference between 1st wave and the 2nd wave is ${\varphi _{1,2}} = 45^\circ $
And, The path difference between the 1st wave and the 3rd wave is $\dfrac{\lambda }{4}$.
$\therefore {\varphi _{1,3}} = \dfrac{{2\pi }}{\lambda } \times \dfrac{\lambda }{4} = \dfrac{\pi }{2}$
So, the diagram will be,

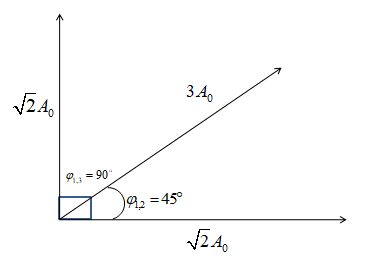
Now, if we calculate the resultant amplitude of the 1st and 3rd waves, the direction will be along with the 2nd wave.
\[{A_{{R_{1,3}}}} = \sqrt {{A_1}^2 + {A_3}^2 + 2{A_1}{A_3}\cos {\varphi _{1,3}}} \]
Given, ${A_1} = \sqrt 2 {A_0}$and ${A_3} = \sqrt 2 {A_0}$
\[ \Rightarrow {A_{{R_{1,3}}}} = \sqrt {{{\left( {\sqrt 2 {A_0}} \right)}^2} + {{\left( {\sqrt 2 {A_0}} \right)}^2} + 2 \times \sqrt 2 {A_0} \times \sqrt 2 {A_0}\cos \dfrac{\pi }{2}} \]
\[ \Rightarrow {A_{{R_{1,3}}}} = \sqrt {4{A_0}^2} \]
\[ \Rightarrow {A_{{R_{1,3}}}} = 2{A_0}\]

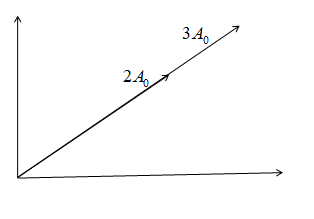
Now the resultant amplitude will be, ${A_R} = \sqrt {{{\left( {2{A_0}} \right)}^2} + {{\left( {3{A_0}} \right)}^2} + 2 \times \left( {2{A_0}} \right) \times \left( {3{A_0}} \right)\cos 0} $
$ \Rightarrow {A_R} = \sqrt {4{A_0}^2 + 9{A_0}^2 + 12{A_0}^2} $
$ \Rightarrow {A_R}^2 = 25{A_0}^2$
The intensity $I \propto {A^2}$ , $A = $ amplitude.
So, here the intensity ${I_0} \propto {A_0}^2$
Hence, the answer will be ${I_{net}} = 25{I_0}$.

Note: In physics, two wave sources are said to be coherent if their frequency and waveform are the same and the phase difference between them is fixed. Coherence is an ideal characteristic of waves that creates stationary (i.e. temporally and spatially constant) interference.
> Laser light is a coherent source of light. The light from the laser light has an identical frequency and phase.
> Sound waves are also examples of coherent sources. The electrical signals emitting from the sound waves traverse with a similar frequency and phase.