
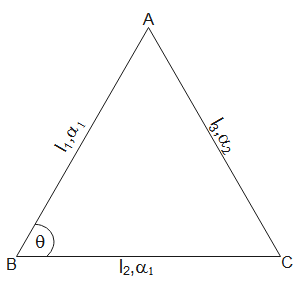
Three rods A, B and C form an equilateral triangle at ${{0}^{{}^\circ }}C$. Rods AB and BC have the same coefficient of expansion $\alpha_1$ and rod AC has $\alpha_2$. If change in angle between AB and BC is $d\theta $. Then what is the temperature through which the system is heated.
A. $\dfrac{\sqrt{2}d\theta }{3\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)}$
B. $\dfrac{\sqrt{3}d\theta }{2\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)}$
C. $\dfrac{\sqrt{2}d\theta }{5\left( 2{{\alpha }_{2}}-{{\alpha }_{1}} \right)}$
D. $\dfrac{\sqrt{3}d\theta }{\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)}$

Answer
556.8k+ views
Hint: Use cosine law to determine the equation for triangle ABC. Differentiate this equation. Change in length of each rod can be written in terms of its thermal coefficient. Substitute the value of change in length in differentiated equations. Rearrange the equation to obtain the temperature through which the system is heated.
Complete step by step answer:
In the triangle ABC, using cosine law, we have
$C{{A}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB.BC\cos \theta $
Initially, the triangle formed by the rods is equilateral and $\theta ={{60}^{{}^\circ }}$.
Let us assume that the lengths of AB, BC and CA is ${{l}_{1}}$, ${{l}_{2}}$ and ${{l}_{3}}$ respectively. Then from cosine formula, we have
$l_{3}^{2}=l_{1}^{2}+l_{2}^{2}-2{{l}_{1}}{{l}_{2}}cos\theta $ ….. (1)
This implies that,
$\cos \theta =\dfrac{l_{1}^{2}+l_{2}^{2}-l_{3}^{2}}{2{{l}_{1}}{{l}_{2}}}$
On differentiating equation (1), we have
$2{{l}_{3}}d{{l}_{3}}=2{{l}_{1}}d{{l}_{1}}+2{{l}_{2}}d{{l}_{2}}-2\cos \theta \left( {{l}_{2}}d{{l}_{1}}+{{l}_{1}}d{{l}_{2}} \right)+2{{l}_{1}}{{l}_{2}}\sin \theta d\theta $
$2ld{{l}_{3}}=2ld{{l}_{1}}+2ld{{l}_{2}}-2l\cos \theta \left( d{{l}_{1}}+d{{l}_{2}} \right)+2{{l}^{2}}\sin \theta d\theta $
$d\theta =\dfrac{d{{l}_{3}}-d{{l}_{1}}-d{{l}_{2}}+\cos \theta \left( d{{l}_{1}}+d{{l}_{2}} \right)}{l\sin \theta }$ ….. (2)
In this problem, the triangle is equilateral. Therefore, ${{l}_{1}}={{l}_{2}}={{l}_{3}}=l(say)$
When temperature of the system is increased, the dimensions of rods change due to linear thermal expansion. Change in length of the rod having coefficient of expansion $\alpha$, due to change in temperature $\Delta T$ is given by
$dl=\alpha l\Delta T$
We are given that, rods AB and BC have the same coefficient of expansion $\alpha_1$ and rod AC has $\alpha_2$.
Now from above equation, we have
$d{{l}_{1}}={{\alpha }_{1}}l\Delta T$
$d{{l}_{2}}={{\alpha }_{1}}l\Delta T$
$d{{l}_{3}}={{\alpha }_{2}}l\Delta T$
Substituting these values in (2), we get
$d\theta =\dfrac{{{\alpha }_{2}}l\Delta T-{{\alpha }_{1}}l\Delta T-{{\alpha }_{1}}l\Delta T+\cos {{60}^{{}^\circ }}\left( {{\alpha }_{1}}l\Delta T+{{\alpha }_{1}}l\Delta T \right)}{l\sin {{60}^{{}^\circ }}}$
This implies that,
$d\theta =\dfrac{{{\alpha }_{2}}\Delta T-{{\alpha }_{1}}\Delta T}{\dfrac{\sqrt{3}}{2}}=\dfrac{2\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)\Delta T}{\sqrt{3}}$
On rearranging this equation, we get
$\Delta T=\dfrac{\sqrt{3}d\theta }{2({{\alpha }_{2}}-{{\alpha }_{1}})}$
Now, we can conclude that the temperature through which the system is heated is $\Delta T=\dfrac{\sqrt{3}d\theta }{2({{\alpha }_{2}}-{{\alpha }_{1}})}$.
Hence, option B is correct.
Note: When temperature of a substance is increased, its dimensions change. This is known as thermal expansion. For a linear expansion, change in length is linearly proportional to coefficient of thermal expansion and increase in temperature.
Complete step by step answer:
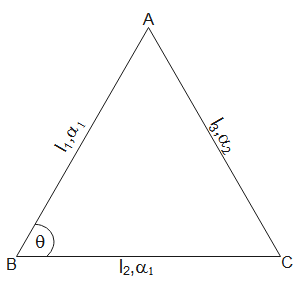
In the triangle ABC, using cosine law, we have
$C{{A}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB.BC\cos \theta $
Initially, the triangle formed by the rods is equilateral and $\theta ={{60}^{{}^\circ }}$.
Let us assume that the lengths of AB, BC and CA is ${{l}_{1}}$, ${{l}_{2}}$ and ${{l}_{3}}$ respectively. Then from cosine formula, we have
$l_{3}^{2}=l_{1}^{2}+l_{2}^{2}-2{{l}_{1}}{{l}_{2}}cos\theta $ ….. (1)

This implies that,
$\cos \theta =\dfrac{l_{1}^{2}+l_{2}^{2}-l_{3}^{2}}{2{{l}_{1}}{{l}_{2}}}$
On differentiating equation (1), we have
$2{{l}_{3}}d{{l}_{3}}=2{{l}_{1}}d{{l}_{1}}+2{{l}_{2}}d{{l}_{2}}-2\cos \theta \left( {{l}_{2}}d{{l}_{1}}+{{l}_{1}}d{{l}_{2}} \right)+2{{l}_{1}}{{l}_{2}}\sin \theta d\theta $
$2ld{{l}_{3}}=2ld{{l}_{1}}+2ld{{l}_{2}}-2l\cos \theta \left( d{{l}_{1}}+d{{l}_{2}} \right)+2{{l}^{2}}\sin \theta d\theta $
$d\theta =\dfrac{d{{l}_{3}}-d{{l}_{1}}-d{{l}_{2}}+\cos \theta \left( d{{l}_{1}}+d{{l}_{2}} \right)}{l\sin \theta }$ ….. (2)
In this problem, the triangle is equilateral. Therefore, ${{l}_{1}}={{l}_{2}}={{l}_{3}}=l(say)$
When temperature of the system is increased, the dimensions of rods change due to linear thermal expansion. Change in length of the rod having coefficient of expansion $\alpha$, due to change in temperature $\Delta T$ is given by
$dl=\alpha l\Delta T$
We are given that, rods AB and BC have the same coefficient of expansion $\alpha_1$ and rod AC has $\alpha_2$.
Now from above equation, we have
$d{{l}_{1}}={{\alpha }_{1}}l\Delta T$
$d{{l}_{2}}={{\alpha }_{1}}l\Delta T$
$d{{l}_{3}}={{\alpha }_{2}}l\Delta T$
Substituting these values in (2), we get
$d\theta =\dfrac{{{\alpha }_{2}}l\Delta T-{{\alpha }_{1}}l\Delta T-{{\alpha }_{1}}l\Delta T+\cos {{60}^{{}^\circ }}\left( {{\alpha }_{1}}l\Delta T+{{\alpha }_{1}}l\Delta T \right)}{l\sin {{60}^{{}^\circ }}}$
This implies that,
$d\theta =\dfrac{{{\alpha }_{2}}\Delta T-{{\alpha }_{1}}\Delta T}{\dfrac{\sqrt{3}}{2}}=\dfrac{2\left( {{\alpha }_{2}}-{{\alpha }_{1}} \right)\Delta T}{\sqrt{3}}$
On rearranging this equation, we get
$\Delta T=\dfrac{\sqrt{3}d\theta }{2({{\alpha }_{2}}-{{\alpha }_{1}})}$
Now, we can conclude that the temperature through which the system is heated is $\Delta T=\dfrac{\sqrt{3}d\theta }{2({{\alpha }_{2}}-{{\alpha }_{1}})}$.
Hence, option B is correct.
Note: When temperature of a substance is increased, its dimensions change. This is known as thermal expansion. For a linear expansion, change in length is linearly proportional to coefficient of thermal expansion and increase in temperature.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




