Question

Three normals are drawn to the parabola \[{{y}^{2}}=4ax\cos a\] from any point lying on the straight line \[y=b\sin a\]. Prove that the locus of the orthocenter of the triangles formed by the corresponding tangents is the curve \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\], the angle\[\alpha \] being variable.

Answer 1

Hint: Consider \[x=\lambda \] and \[y=\beta \sin \alpha \], thus forming the point of contact with point \[\left( \lambda ,b\sin \alpha \right)\].

Complete step-by-step answer:

Given that the equation of a parabola is \[{{y}^{2}}=4ax\cos a\]

where ‘a’ can be written as, \[{{y}^{2}}=4Ax\] where \[A=a\cos \alpha \].

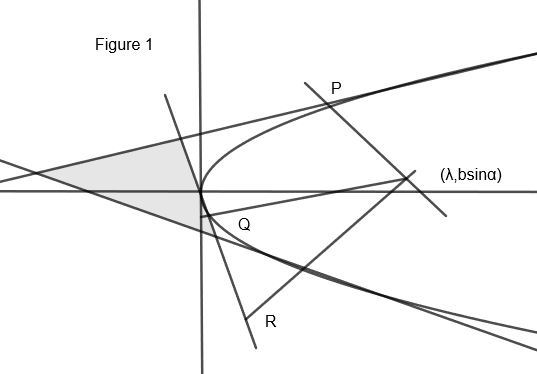
Considering the parabola is drawn, \[{{y}^{2}}=4Ax\] from fig.1.

Let \[P,Q\] and \[R\] be the tangents that are drawn to the parabola.

From the figure, the normal meets at the point \[\left( \lambda ,b\sin \alpha \right)\].

Let the slope be taken by the formula.

\[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=m\]

Let us take the slope \[m=-t\]

The equation of the line perpendicular will get from the equation \[y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)\] for the point \[\left( a{{t}^{2}},2at \right)\] where \[x=a{{t}^{2}},y=2at\]

By substituting the values, we get
\[y-\left( 2at \right)=-t\left( x-\left( a{{t}^{2}} \right) \right)\Rightarrow y-2at=-t\left(
x-a{{t}^{2}} \right)\]

\[\Rightarrow y-2at=-tx+a{{t}^{3}}\]

\[\therefore y+tx=2At+a{{t}^{3}}.....\left( i \right)\]

The coordinates of points of intersection of tangents in a parabola can be found by considering

\[A\left( at_{1}^{2},2a{{t}_{1}} \right),B\left( at_{2}^{2},2a{{t}_{2}} \right)\]

Equation of parabola \[\Rightarrow {{y}^{2}}=4ax\]

The equation of the tangent at \[{{t}_{1}}=y{{t}_{1}}=x+at_{1}^{2}.....\left( i \right)\]

The equation of the tangent at \[{{t}_{2}}=y{{t}_{2}}=x+at_{2}^{2}.....\left( ii \right)\]

\[\left( i \right)-\left( ii \right)\]\[\Rightarrow y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left(
t_{1}^{2}-t_{2}^{2} \right)\]

\[\Rightarrow y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left( {{t}_{1}}-{{t}_{2}} \right)\left(
{{t}_{1}}+{{t}_{2}} \right)\]

\[\therefore y=a\left( {{t}_{1}}+{{t}_{2}} \right)\]

From equation\[\left( i \right)\]\[\Rightarrow y{{t}_{1}}=x+at_{1}^{2}\Rightarrow a\left(
{{t}_{1}}+{{t}_{2}} \right){{t}_{1}}=x+at_{1}^{2}\]

\[at_{1}^{2}+a{{t}_{1}}{{t}_{2}}=x+at_{1}^{2}\Rightarrow x=a{{t}_{1}}{{t}_{2}}\]

\[\therefore \]Point of intersection \[=\left( x,y \right)=\left( a{{t}_{1}}{{t}_{2}},a\left(
 {{t}_{1}}+{{t}_{2}} \right) \right)\]

From fig 1. For point\[\left( \lambda ,b\sin \alpha \right)\], \[y=b\sin \alpha \]and
\[x=\lambda \].

Substituting it on equation \[\left( i \right)\]

\[b\sin \alpha +t\lambda =2At+A{{t}^{3}}\]

By rearranging the above equation, we get

\[A{{t}^{3}}+2At-t\lambda -b\sin \alpha =0\]

\[A{{t}^{3}}+t\left( 2A-\lambda \right)-b\sin \alpha =0\]

Let us consider \[3\]roots as \[{{t}_{1}},{{t}_{2}}\]and \[{{t}_{3}}\]. The algebraic sum of these ordinates is zero.

\[\therefore {{t}_{1}}+{{t}_{2}}+{{t}_{3}}=0\]

Similarly, the perpendicular to the normal, i.e. product of the root of the slope.

\[{{t}_{1}}{{t}_{2}}{{t}_{3}}=\dfrac{b\sin \alpha }{A}\]

Let us consider \[\left( h,k \right)\]as \[\left( x,y \right)\]

\[h=-A=-a\cos \alpha .....\left( ii \right)\]

\[k=A\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{1}}.{{t}_{2}}.{{t}_{3}} \right)=A\left(
0+\dfrac{b\sin \alpha }{A} \right)\]

\[\therefore k=b\sin \alpha ....\left( iii \right)\]

\[\left( h,k \right)=\left( x,y \right)\]

\[\therefore x=-a\cos \alpha \]and \[y=b\sin \alpha \]

Therefore from \[\left( i \right)\]and \[\left( ii \right)\], we get the locus as

\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]

Note: The focal distance of a point \[\left( x,y \right)\]on the ellipse
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]is constant and equal to the
length of the major axis.