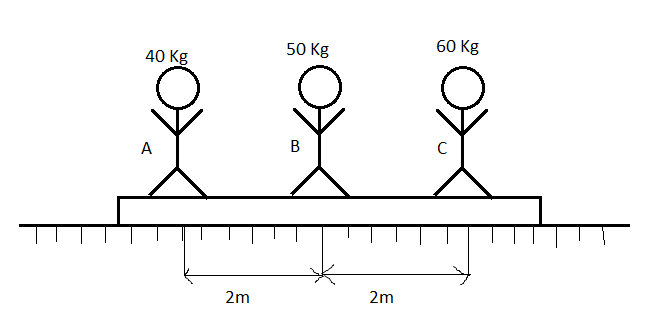
Three men, A,B and C of mass $40kg$, $50kg$ and $60kg$ are standing on a plank of mass $90kg$, which is kept on a smooth horizontal plane. If A and C exchange their positions, then B will shift:
A. $1/3m$ towards left w.r.t ground
B. $1/3m$ towards right w.r.t ground
C. Will not move w.r.t ground
D. $5/3m$ towards left w.r.t to ground
Answer
Verified591.6k+ views
Hint: When no external force acts on a system, the center of mass of the system remains constant. This problem can be solved using the concept that since there are no external forces on the system, the center of mass of the system will remain the same. By equating the centers of mass for the initial and final conditions we can find the shift in the position of B.
Formula used:
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$
where ${{r}_{x}}$ and ${{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass m with respect to $\left( x,y \right)$.
Complete Step-by-Step solution:
In this problem, since all the men are assumed to be equal in height and movement of the plank is only allowed in the horizontal plane, the center of mass in the vertical direction is not of required importance in solving the question.
We will consider the three men along with the plank to be the system.
Hence, we will solve this problem only in one dimension (the horizontal) to make it easier.
Hence, let B be the origin (0) and the direction towards C (right) be considered the positive axis.
The plank can be considered to be a point mass with all its mass concentrated at its center of mass (which will be the origin as it is the midpoint and the center of mass of a uniform rectangle (cuboid in 2 dimensions is its center)
Now, position of C with respect to B =$2m$ ---------------(1)
Mass of C is given to be ${{M}_{C}}=60Kg$ -----------------(2)
Now, position of A with respect to B =$-2m$------------- --(3)
Mass of A is given to be ${{M}_{A}}=40Kg$ ------------------(4)
Now, position of B with respect to B =$0m$ ------------------(5)
Mass of B is given to be ${{M}_{B}}=50Kg$ ---------------------(6)
Position of point mass of plank with respect to B =$0m$--------------------(7)
Mass of plank is given to be ${{M}_{Plank}}=90Kg$ ------------------(8)
Now, we will find the center of mass w.r.t point B.
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$ where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$ -------------(9)
where ${{r}_{x}} $ and $ {{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass m with respect to $\left( x,y \right)$.
Hence, using (1),(2),(3),(4),(5),(6), (7), (8) and (9) , we get center of mass in the horizontal direction $\left( {{P}_{1}} \right)$ as
${{P}_{1}}=\dfrac{\left( {{M}_{A}}\times \left( -2 \right) \right)+\left( {{M}_{B}}\times \left( 0 \right) \right)+\left( {{M}_{C}}\times \left( 2 \right) \right)+\left( {{M}_{Plank}}\times \left( ) \right) \right)}{{{M}_{A}}+{{M}_{B}}+{{M}_{C}}+{{M}_{Plank}}}$
$\therefore {{P}_{1}}=\dfrac{\left( 40\times \left( -2 \right) \right)+\left( 50\times \left( 0 \right) \right)+\left( 60\times \left( 2 \right) \right)+\left( 90\times \left( 0 \right) \right)}{40+50+60+90}=\dfrac{-80+0+120+0}{240}=\dfrac{40}{240}=\dfrac{1}{6}m$ ------------(10)
Hence, the center of mass of the system is at a distance of $\dfrac{1}{6}m$ from B towards C.
Now, it is given in the question that A and C exchange positions. Hence, the center of mass relative to point B will also change. Hence, due to this plank shifts horizontally to the right by x. Hence,
Now, position of C with respect to earlier position of B, i.e. origin =$\left( -2+x \right)m$ - ---------------------(11)
Mass of C is given to be ${{M}_{C}}=60Kg$ -------------(12)
Now, position of A with respect to earlier position of B, i.e. origin = $\left( 2+x \right)m$ ---------------------(13)
Mass of A is given to be ${{M}_{A}}=40Kg$ ----------------(14)
Now, position of B with respect to earlier position of B, i.e. origin =$\left( x \right)m$ ---------------(15)
Mass of B is given to be ${{M}_{B}}=50Kg$ --------------------(16)
Position of point mass of plank with respect to earlier position of B = $\left( x \right)m$--------------------------(17)
Mass of plank is given to be ${{M}_{Plank}}=90Kg$ -------------(18)
Again using (9),(10),(11),(12),(13),(14), (15),(16),(17) and(18) we will get the new center of mass of the system $\left( {{P}_{2}} \right)$ as:
${{P}_{2}}=\dfrac{\left( {{M}_{A}}\times \left( 2+x \right) \right)+\left( {{M}_{B}}\times \left( x \right) \right)+\left( {{M}_{C}}\times \left( -2+x \right) \right)+\left( {{M}_{Plank}}\times \left( x \right) \right)}{{{M}_{A}}+{{M}_{B}}+{{M}_{C}}+{{M}_{Plank}}}$
\[\therefore {{P}_{2}}=\dfrac{\left( 40\times \left( 2+x \right) \right)+\left( 50\times \left( x \right) \right)+\left( 60\times \left( -2+x \right) \right)+\left( 90\times \left( x \right) \right)}{40+50+60+90}\]
\[\therefore {{P}_{2}}=\dfrac{\left( 80+40x \right)+\left( 50x \right)+\left( -120+60x \right)+90x}{40+50+60+90}=\dfrac{-40+240x}{240}=\dfrac{24x-4}{24}=\dfrac{6x-1}{6}m\] ---------------------(19)
Now, since there are no external forces on the system but the change has occurred due to internal actions (exchange of positions between two masses of the system), the center of mass in the initial and final state must remain the same with respect to the origin.
Hence, from (10) and (19)
$\dfrac{1}{6}=\dfrac{6x-1}{6}$
$\therefore 1=6x-1$
$\therefore 2=6x$
$\therefore x=\dfrac{1}{3}m$
Hence, the plank shifts by $\dfrac{1}{3}m$ towards the right with respect to the ground.
Hence, the correct option is B) $1/3m$ towards right w.r.t ground.
Note: Students can make a very common silly mistake of not considering the mass of the plank in the problem since it does not hit the mind at the first sight of the question intuitively. Upon seeing the figure also, (which only contains the numerical values of the masses of the three men), students may quite easily forget about the mass of the plank and proceed only using the masses of the three men for finding out the center of mass.
However, this leads to a completely wrong result and a lot of wastage of time. Students should be careful of such intricacies in such problems specially.
Formula used:
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$
where ${{r}_{x}}$ and ${{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass m with respect to $\left( x,y \right)$.
Complete Step-by-Step solution:
In this problem, since all the men are assumed to be equal in height and movement of the plank is only allowed in the horizontal plane, the center of mass in the vertical direction is not of required importance in solving the question.
We will consider the three men along with the plank to be the system.
Hence, we will solve this problem only in one dimension (the horizontal) to make it easier.
Hence, let B be the origin (0) and the direction towards C (right) be considered the positive axis.
The plank can be considered to be a point mass with all its mass concentrated at its center of mass (which will be the origin as it is the midpoint and the center of mass of a uniform rectangle (cuboid in 2 dimensions is its center)
Now, position of C with respect to B =$2m$ ---------------(1)
Mass of C is given to be ${{M}_{C}}=60Kg$ -----------------(2)
Now, position of A with respect to B =$-2m$------------- --(3)
Mass of A is given to be ${{M}_{A}}=40Kg$ ------------------(4)
Now, position of B with respect to B =$0m$ ------------------(5)
Mass of B is given to be ${{M}_{B}}=50Kg$ ---------------------(6)
Position of point mass of plank with respect to B =$0m$--------------------(7)
Mass of plank is given to be ${{M}_{Plank}}=90Kg$ ------------------(8)
Now, we will find the center of mass w.r.t point B.
The center of mass of a system relative to a point $\left( x,y \right)$ is given by $\left( {{C}_{x}},{{C}_{y}} \right)$ where
$\left( {{C}_{x}},{{C}_{y}} \right)=\left( \dfrac{\sum{m{{r}_{x}}}}{\sum{m}},\dfrac{\sum{m{{r}_{y}}}}{\sum{m}} \right)$ -------------(9)
where ${{r}_{x}} $ and $ {{r}_{y}}$ are the positions in the horizontal and vertical plane of the mass m with respect to $\left( x,y \right)$.
Hence, using (1),(2),(3),(4),(5),(6), (7), (8) and (9) , we get center of mass in the horizontal direction $\left( {{P}_{1}} \right)$ as
${{P}_{1}}=\dfrac{\left( {{M}_{A}}\times \left( -2 \right) \right)+\left( {{M}_{B}}\times \left( 0 \right) \right)+\left( {{M}_{C}}\times \left( 2 \right) \right)+\left( {{M}_{Plank}}\times \left( ) \right) \right)}{{{M}_{A}}+{{M}_{B}}+{{M}_{C}}+{{M}_{Plank}}}$
$\therefore {{P}_{1}}=\dfrac{\left( 40\times \left( -2 \right) \right)+\left( 50\times \left( 0 \right) \right)+\left( 60\times \left( 2 \right) \right)+\left( 90\times \left( 0 \right) \right)}{40+50+60+90}=\dfrac{-80+0+120+0}{240}=\dfrac{40}{240}=\dfrac{1}{6}m$ ------------(10)
Hence, the center of mass of the system is at a distance of $\dfrac{1}{6}m$ from B towards C.
Now, it is given in the question that A and C exchange positions. Hence, the center of mass relative to point B will also change. Hence, due to this plank shifts horizontally to the right by x. Hence,
Now, position of C with respect to earlier position of B, i.e. origin =$\left( -2+x \right)m$ - ---------------------(11)
Mass of C is given to be ${{M}_{C}}=60Kg$ -------------(12)
Now, position of A with respect to earlier position of B, i.e. origin = $\left( 2+x \right)m$ ---------------------(13)
Mass of A is given to be ${{M}_{A}}=40Kg$ ----------------(14)
Now, position of B with respect to earlier position of B, i.e. origin =$\left( x \right)m$ ---------------(15)
Mass of B is given to be ${{M}_{B}}=50Kg$ --------------------(16)
Position of point mass of plank with respect to earlier position of B = $\left( x \right)m$--------------------------(17)
Mass of plank is given to be ${{M}_{Plank}}=90Kg$ -------------(18)
Again using (9),(10),(11),(12),(13),(14), (15),(16),(17) and(18) we will get the new center of mass of the system $\left( {{P}_{2}} \right)$ as:
${{P}_{2}}=\dfrac{\left( {{M}_{A}}\times \left( 2+x \right) \right)+\left( {{M}_{B}}\times \left( x \right) \right)+\left( {{M}_{C}}\times \left( -2+x \right) \right)+\left( {{M}_{Plank}}\times \left( x \right) \right)}{{{M}_{A}}+{{M}_{B}}+{{M}_{C}}+{{M}_{Plank}}}$
\[\therefore {{P}_{2}}=\dfrac{\left( 40\times \left( 2+x \right) \right)+\left( 50\times \left( x \right) \right)+\left( 60\times \left( -2+x \right) \right)+\left( 90\times \left( x \right) \right)}{40+50+60+90}\]
\[\therefore {{P}_{2}}=\dfrac{\left( 80+40x \right)+\left( 50x \right)+\left( -120+60x \right)+90x}{40+50+60+90}=\dfrac{-40+240x}{240}=\dfrac{24x-4}{24}=\dfrac{6x-1}{6}m\] ---------------------(19)
Now, since there are no external forces on the system but the change has occurred due to internal actions (exchange of positions between two masses of the system), the center of mass in the initial and final state must remain the same with respect to the origin.
Hence, from (10) and (19)
$\dfrac{1}{6}=\dfrac{6x-1}{6}$
$\therefore 1=6x-1$
$\therefore 2=6x$
$\therefore x=\dfrac{1}{3}m$
Hence, the plank shifts by $\dfrac{1}{3}m$ towards the right with respect to the ground.
Hence, the correct option is B) $1/3m$ towards right w.r.t ground.
Note: Students can make a very common silly mistake of not considering the mass of the plank in the problem since it does not hit the mind at the first sight of the question intuitively. Upon seeing the figure also, (which only contains the numerical values of the masses of the three men), students may quite easily forget about the mass of the plank and proceed only using the masses of the three men for finding out the center of mass.
However, this leads to a completely wrong result and a lot of wastage of time. Students should be careful of such intricacies in such problems specially.
Recently Updated Pages
There are four balls of different colors and four boxes class 10 maths CBSE
How many sides does a tetrahedron have class 10 maths CBSE
How does the moons gravity differ from the earths class 10 physics CBSE
Electrical Pressure is also called A Current B Voltage class 10 physics CBSE
The most densely Populated country of the world is class 10 social studies CBSE
The arithmetic mean of 12 observations is 75 If the class 10 maths CBSE
Trending doubts
The shortest day of the year in India
Why is there a time difference of about 5 hours between class 10 social science CBSE
Write a letter to the principal requesting him to grant class 10 english CBSE
What is the median of the first 10 natural numbers class 10 maths CBSE
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths
State and prove converse of BPT Basic Proportionality class 10 maths CBSE