Question

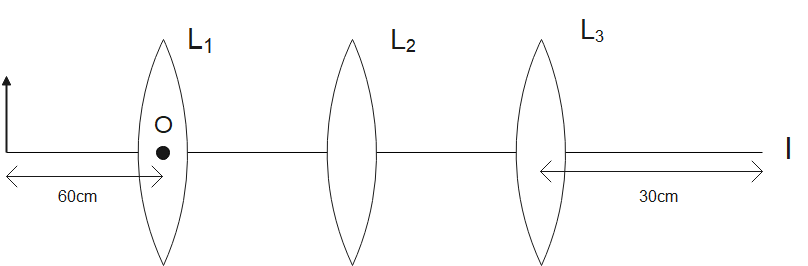
Three lenses ${{L}_{1}},{{L}_{2}},{{L}_{3}}$ each of focal length 30cm are placed co-axially as shown in figure. An object is held at 60cm from the optic center of lens ${{L}_{1}}$. The final real image is formed at the focus of ${{L}_{3}}$. Calculate separation between (i) ${{L}_{1}}$ and ${{L}_{2}}$ (ii) ${{L}_{2}}$ and ${{L}_{3}}$

Answer 1

Hint: In any question of optics, we always measure distance from the optical center of the lens or the mirror. To solve any question, we must remember where the image will be formed if the object is placed at focus or infinity or 2f. This will save our time, but if someday we forget about this, we can always use lens formula to find the distance of the image.

Complete step by step answer:
In this question we have been given with three lenses ${{L}_{1}},{{L}_{2}},{{L}_{3}}$ each of them having a focal length of 30cm
An object is placed at 60cm from the center of lens ${{L}_{1}}$
We need to find the distance between the lenses
Now according to the question the focal length of each lens is 30cm and the object is placed at 60 cm. this means that the object is placed at 2f distance (twice of focal length). We know that when an object is placed at 2f (left side of lens) the image formation also takes place at 2f (on right side of lens). This means that the image will be formed at 60cm on the right side of the lens ${{L}_{1}}$.
Now for the lens ${{L}_{3}}$ , The image is formed at 30cm on the right side of lens ${{L}_{3}}$, While the lens ${{L}_{3}}$ have a focal length of 30 cm. This means that the image is formed at the focal distance of the lens on the right side.
We know that to form an image on the focus the incident rays of light must incident parallel to the lens, So, we can say that the Rays incident on the lens ${{L}_{3}}$ are parallel to each other as this is the only way to make image at the focal point of lens
For lens ${{L}_{2}}$ the image should be formed at the focus of lens ${{L}_{2}}$ because this is the only way by which rays can travel in parallel.
So, the above image now becomes

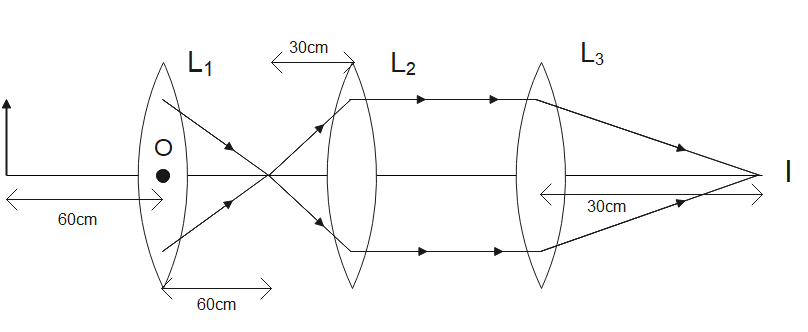
Now we can say that the distance between lens ${{L}_{1}}$ and ${{L}_{2}}$ is 60 cm + 30 cm = 90 cm
But we cannot determine the distance between lens ${{L}_{2}}$ and ${{L}_{3}}$ because the parallel rays can travel infinite distance and can still remain parallel and it can be possible that lens ${{L}_{2}}$ and ${{L}_{3}}$ are sticked together.
So, there is no fixed distance, but we can say that the distance between lens ${{L}_{2}}$ and ${{L}_{3}}$ can vary from 0 to $\infty $

Note: We cannot determine the distance between lens ${{L}_{2}}$ and ${{L}_{3}}$ because the parallel rays can travel infinite distance and can still remain parallel and it can be possible that lens ${{L}_{2}}$ and ${{L}_{3}}$ are sticked together so in this type of situation, we provide a range of distance as a solution of the question.